Horizontal Oscillation of a Mass Attached to an Ideal Spring

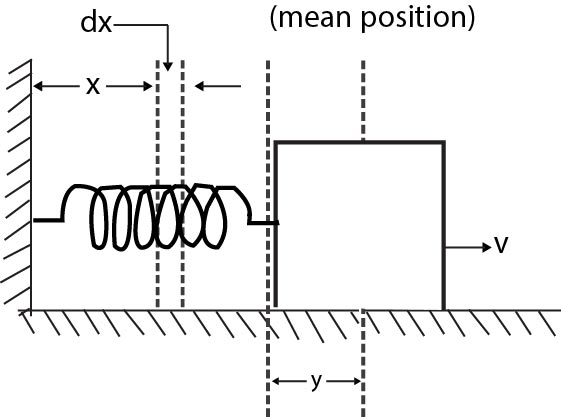
Consider a block of mass m, attached to one end of a massless spring, obeying Hooke's law, with its other end attached to a rigid support. The block rests on a horizontal frictionless surface. (Figure)
Let the block be slightly pulled towards right and left free to oscillate. It executes SHM. Consider the position of the block, at any instant, when its displacement is 'x' from the mean position. The net force acting upon the block is the restoring force due to spring, (towards left).
Thus `vecF = -kvecx` [where 'k' is the force constant]
or `veca = vecF/m = = k/m (vecx)`
Comparing with the standard from `vecF= - omega^2vecx`
We have `omega^2 =k/m`
Now, time period of motion
`T = (2 pi)/omega = 2 pi sqrt(m/k)`
Let the block be slightly pulled towards right and left free to oscillate. It executes SHM. Consider the position of the block, at any instant, when its displacement is 'x' from the mean position. The net force acting upon the block is the restoring force due to spring, (towards left).
Thus `vecF = -kvecx` [where 'k' is the force constant]
or `veca = vecF/m = = k/m (vecx)`
Comparing with the standard from `vecF= - omega^2vecx`
We have `omega^2 =k/m`
Now, time period of motion
`T = (2 pi)/omega = 2 pi sqrt(m/k)`