Physics PROJECTILE MOTION

Projectile Fired from Bottom of Inclined Plane

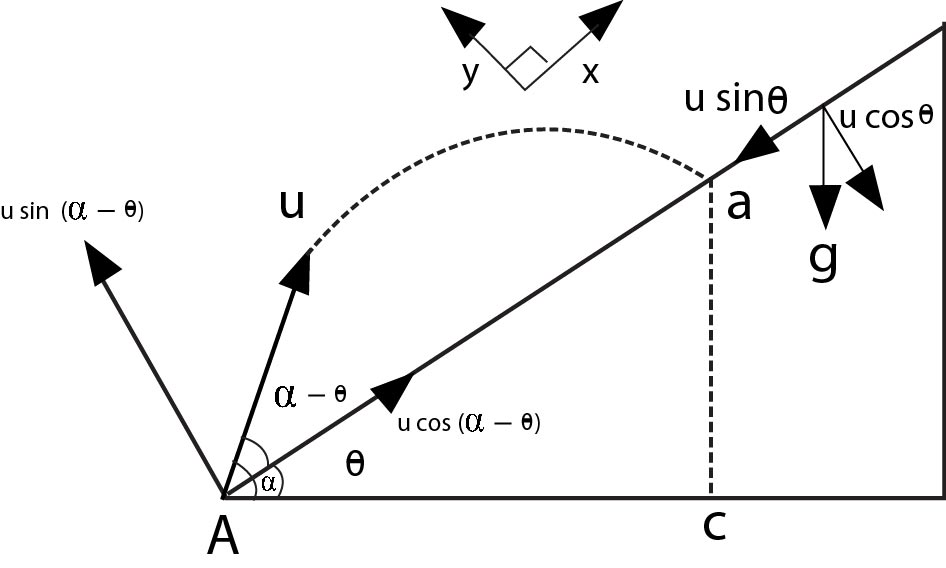
Consider a particle fired with speed u from bottom of an inclined plane. The angle of projection with the horizontal is `alpha` & angle made by incline with horizontal is `theta`.

As shown in figure, `x` & `y` direction will be along incline& perpendicular to incline, respectively. Point of projection is `A` & point where the particle strikes incline is `B`

Displacement is `AB` along `x`- axis
Displacement in `y` direction is zero.

`text(Time of flight :)`

Apply `S = ut + 1/2 a t^2` along `y- ` axis

`0 = u sin (alpha -theta) T - 1/2g cos theta T^2`

Time of flight `T = (2u sin(alpha -theta))/(g cos theta)`

`text(Range along incline :)`

Length All is the range
Horizontal displacement in time `T`

`AC = u cos alpha T =(2usin(alpha-theta) xx u cos alpha)/(g cos theta)`

Range along incline `= AB =(AC)/(cos theta)`

`AB= (2u^2 cos alpha sin(alpha- theta))/(g cos^2 theta)`

`text(Alternative method for range :)`

To find AB, apply `s= ut +1/2 at^2` along x direction

`AB = u cos (alpha- theta)T -1/2 g sin theta T^2`

Put `T = (2u sin(alpha-theta))/(g cos theta)`

`AB=(2u^2sin(alpha-theta))/(gcos^2theta)`

`text(Value of)` `alpha` `text(for maximum range :)`

Range `= AB = (u^2(sin(2 alpha -theta)- sin theta))/(g cos^2 theta)`

For a given u & `theta` for maximum range

`sin(2 alpha - theta) =1 ` implies `(2 alpha- theta) = pi/2`

or `alpha = pi/4 +theta/2`

`R_(max) =(u^2(1-sin theta))/(g cos^2 theta) = u^2/(g(1+sin theta))`

`text(The two values of u to get the some range along inclined plane ( u = constant) :)`

Range `= AB = (u^2(sin(2 alpha-theta) - sin theta))/(g cos^2 theta)`

Leg `alpha_1` & `alpha_2` be the 2 angle to give the same range

`sin (2 alpha_1 - theta) = sin(pi-(2 alpha_2-theta)), 2 alpha_2-theta= pi-2 alpha_2 +theta`

`alpha_1+alpha_2 = pi/2 +theta`

There are two angles of projection for which we obtain the same range along incline for the same speed

of projection such that `alpha_1 +alpha_2 =pi/2 +theta`

(e) Time of flight `=(2 u sin(alpha- theta))/(g cos theta)`

Projectile Fired from Top of Inclined Plane.

The results in this case are the same as results for projectile projected from the bottom of !he incline, except that `theta` is to be replaced by `- theta`

`text(Summary of various results for projectile fired from top of inclined plane :)`

`(a)` Range `AB = (2u^2cos alpha sin(alpha+theta))/(g cos^2 theta)`

`(b)` Condition for maximum range `alpha= pi/2 -theta/2`

`(c)` Value of maximum range `= u^2/(g(1- sin theta))`

`(d)` Relation between the `2` angles of projection to get
same range. (keeping `u` constant)

`alpha_1+alpha_2 =pi/2- theta`

`(e)` Time of flight `= (2u sin(alpha+theta))/(g cos theta)`

Projectile with Variable Acceleration

Suppose a projectile moves in the two dimensional plane with velocity `v = a hati + bx hatj` where `a` and `b` are constant. Initially consider the particle to be situated at origin i.e. at `t =0, x =0` & `y =0` . Now Jet us first find out the equation of trajectory of the projectile. So,

`v= a hat i +b x hat j`

`v_x =a` and `v_y=bx`

But `v_x =(dx)/(dt) =a` and `(dy)/(dt) = v_y=bx`

`dx =a dt`

`int_(x=0)^(x=x) dx = int_(t=0)^(t=t) a dt, [x]_0^x =a[t]_0^t ,`

`x = at..........(1)`

`dy = bx dt`

On substituting value of `x` we have

`dy = b at dt`

`int_(y=0)^(y=y)dy = int_(t=0)^(t=t)b at dt ` `=> [y]_0^y = ba[t^2/2]_0^t`

On integrating `y = (abt^2)/2..............(2)`

Eliminating t between equation 1 and equation 2

`=> (ab)/2 (x/a)^2 => y= (bx^2)/(2a)`

This is the equation of trajectory of the projectile.