Physics CALCULUS FOR PHYSICS

Please Wait... While Loading Full Video

CALCULUS FOR PHYSICS

DIFFERENTIATION

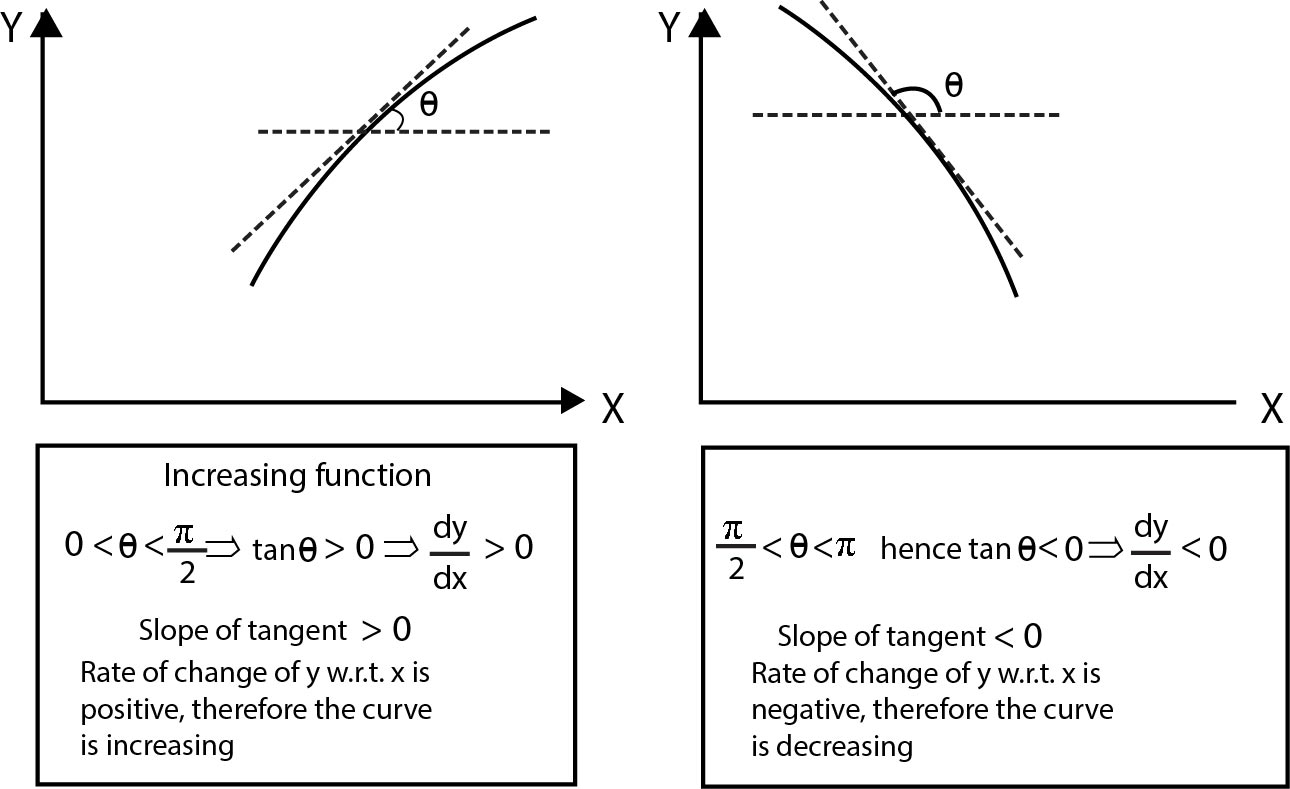
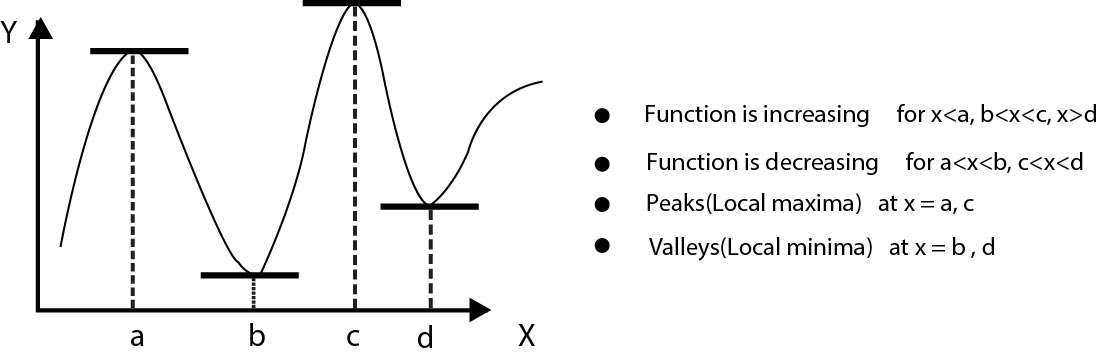
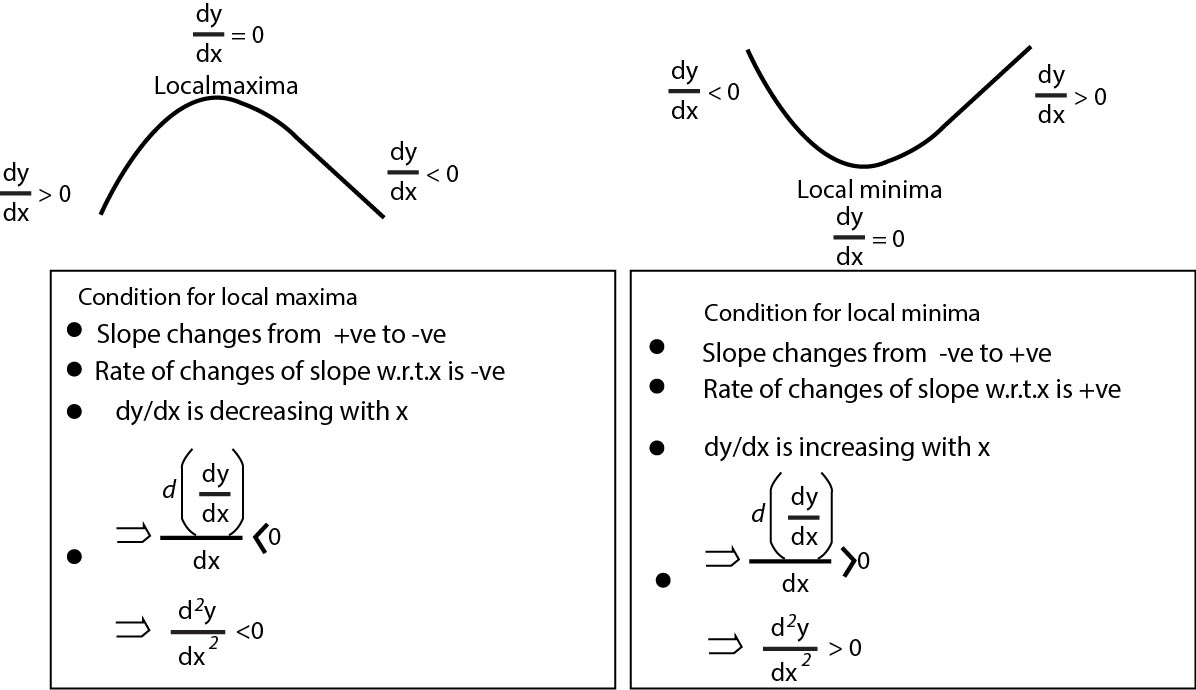
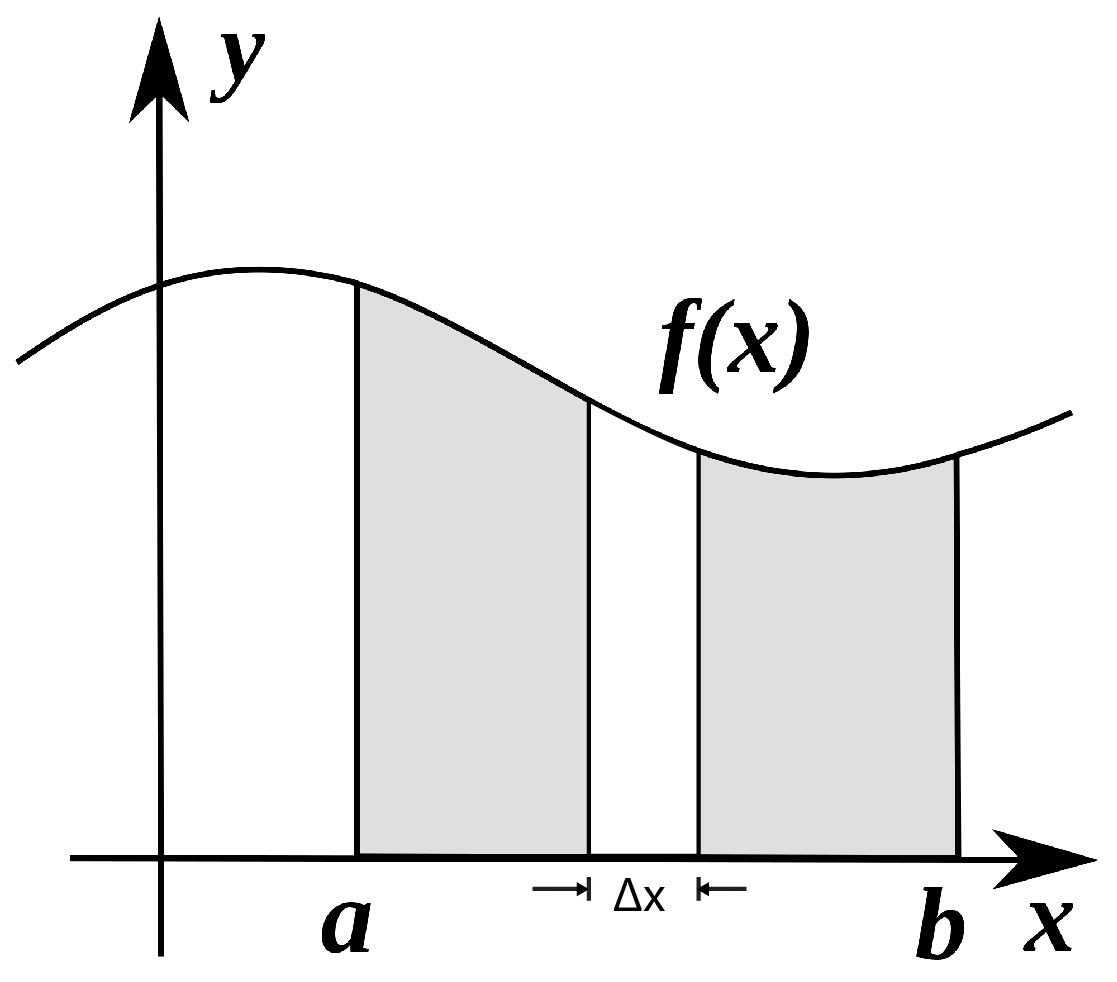
The purpose of differential calculus is to study the nature (i.e., increase or decrease) and the amount of variation in a quantity when another quantity (on which first quantity depends) varies independently.

`text(Quantity :)`
Anything which can be measured is called a quantity.

`text(Constant :)`
A quantity, whose value remains unchanged during mathematical operations, is called a constant quantity. The integers, numbers like,e, etc are all constants.

`text(Variable :)`
A quantity which can have any numerical value between certain specified limit is called as variable.

`text(Function :)`
A quantity y is called a function of a variable x, if corresponding to any given value of x, there exists a single definite value of y. The phrase "y is function of x" is represented as ,`y=f(x)`

For example, consider that y is a function of the variable x which is given by

`y = 3x^2 +7x +2`

If `x = 1,` then `y = 3(1)^2 + 7(1) +2 =12`

and when `x=2,y=3(2^2) +7(2) +2 = 28`

Therefore, when the value of variable x is changed, the value of the function y also changes. But corresponding to each value of x, we get a single definite value of y. Hence, `y = 3x^2 +7x +2` represents a function of `x` .

`text(Meaning of limit)`

Rabbit A wants to reach rabbit B, which sits stationary. A jumps half the distance remaining between them every second. How soon does the rabbit A reach its goal?

Never! (Assuming both rabbits to be point objects)

The gap remaining between them becomes infinitesimal ( i.e. very very small) after a long time.

- It is not a number, that can be expressed. It is smaller than the smallest positive number, that you can think of. The gap `Deltax->0` or it is dx. (dx denotes a very very small change in x.) and is represented as `lim_(x->0)` (read as limit of delta x tends to zero)

- Rabbit A tends to rabbit B.

- Rabbit A's limit is rabbit B.

`text(Slope of secant)`

Consider a curve where the variation of a function `y = f(x)` is plotted with respect to variable x. let P and Q be two points on the curve. The segment PQ is called as secant.

The slope of the secant: slope `= tan theta = (Delta y)/(Delta x)`

(Slope is defined as tan of angle between line and positive x -axis taken counter - clockwise )

`text(Geometric Meaning of Derivative)`

- let P go closer to Q. When the gap between P and Q becomes infinitesimal (very very small), the secant can be approximated as tangent

Hence, `(dy)/(dx)` (or `f'(x)` ) at any point represents the rate of change of y (or f(x)) with respect to x at that point and is also known as derivative of y w.r.t. x.

Physical Meaning of : `(dy)/(dx)`

1. The ratio of change in the function y to change in variable x is called the average rate of change of y

w.r.t.x. For example, if a body covers a distance `Delta s` in
time `Delta t` then average velocity of the body, `v_(Delta t) =(Delta s)/(delta t)` Also,
if the velocity of a body changes by an amount `delta v` in
small time `Delta t` then average acceleration of the body,
`a_(Delta v) = (Delta v)/(Delta t)`

2. The differentiation of a function w.r.t. a variable
implies the instantaneous rate of change of the
function w.r.t. that variable.

Thus, instantaneous velocity of the body, `lim_(Delta t -> 0) (Delta s)/(Delta t) = (ds)/(dt)`

and instantaneous acceleration of the body, `a= lim_(Delta t->0)(Delta v)/(delta t) = (dv)/(dt)`

`(dy)/(dx)` `text(of Functions and their Properties)`

We have found the derivative of , 'with respect to x.
Like wise we can also find derivatives of other functions.Some standard derivatives are as given in the table

`text(Note :)`
In the above table, n and a are constant.

Mathematical operations for derivatives :

`(dK)/(dx) = 0`

`(dK_u)/(dx) = K (du)/(dx)`

`d(u pm v)/(dx) = (du)/(dx) pm (dv)/(dx)`

`(d(uv))/(dx) = u (dv)/(dx) + v (du)/(dx)`

`d(u/v)/(dx) = (v(du)/(dx) - u(dv)/(dx))/v^2`

(Here, K is a constant and u and v are functions of x.)

`text(Increasing and Decreasing Functions)`

NOTE :
A function may not be continuously increasing or decreasing during the entire range (e.g. `sin x, cos x`).

Then we say function is increasing in the range where
`(dy)/(dx) > 0` and decreasing where `(dy)/(dx) < 0`

`text( Local Maxima and Local Minima)`

For local maxima or minima, slope of the curve where it lies must be zero.

So, `(dy)/(dx) =0,` at the point s of local maxima or local minima

Note 2:
Local maxima/minima does not mean that the function has the highest / lowest value at that point. It only means that the function was increasing before and decreasing after that point in case of local maxima and vice-versa in case of minima

`text(Criterion for Local Maxima and Local Minima)`

Note 1:
When we talk of local maxima I minima, we are talking of x: while when we say local maximum value or local minimum value, we are talking of value of y corresponding to that particular local maxima or minima

Note 2:
Local maxima/minima does not mean that the function has the highest / lowest value at that point. It only means that the function was increasing before and decreasing after that point in case of local maxima and vice-versa in case of minima

INTEGRATION

In integral calculus, the differential coefficient of a function is given. We are required to find the function. Thus, integration is the reverse of differentiation.

`int` sign is used for integration. If `I` is integration of f(x) with respect to x then `I = intf(x) dx` and it is read as integration of `f(x)` w.r.t. x is `I`

For example, let us proceed to obtain integral of `x^n` w.r.t. x. We already know that `d/dx(x^(n+1)) = (n+1)x^n`

Since the process of integration is the reverse process of differentiation,

`int(n+1)x^n dx = x^(n+1)` or `intx^n dx = (x^(n+1))/(n+1)`

The above formula holds for all values of `n`, except `n = -1`.
`int 1/x dx = log _e x`

It is because, for `n = -1, int x^-1dx = int 1/x dx ` since `d/(dx) (log_e x)=1/x`

`therefore int 1/x dx =log_e x`

Similarly, the formula for integration of some other functions can be obtained if we know the differential coefficients of various functions.

Basic Integration Formulas

`1.` `int[f(x) pm g(x)]dx = int f(x) dx pm int g(x)dx`

`2.` `intx^n dx = (x^(n+1))/(n+1) +C, n ne -1`

`3.` `int(dx)/x = ln|x| + C`

`4.` `inte^x dx = e^x +C `

`5.` `int sin x dx =-cos x + C`

`6.` `int cos x dx = sin x +C`

`7.` `int tan x dx = ln |sec x| +C`

`8.` `int cot x dx = ln | sin x| +C`

`9.` `int secx dx = ln |sec x +tan x| +C`

`10.` `intcosec x dx = - ln |cosec x + cot x| + C`

`11.` `int sec^2x dx = tan x + c`

`12.` `int cos e c^2x dx = -cot x + C`

`13.` `int sec x tan x dx = sec x +c`

`14.` `int cos e c x cot x dx = -cosx secx +C`

Integration by Substitution�

Suppose we represent an integral by `int f(u)du = F(u) +c` (i.e., `F(u)` is the integral of `f(u)` w.r.t. `u` ).

Now suppose u is a function of `x` given by `u = g(x)` , then `du = g'(x)dx` (where `g'(x)` is `(d (g(x)))/(dx)`) and the above integral can be written as `int f(g(x)), g(x)dx =F (g(x)) +C`

Thus if we have to find the integral given in the form of a function along with its derivative, we can use the above formula to find the integral.

An important result: if `intf(x)dx = F(x) + C `
then

`intf(ax +b) dx = (F(ax +b))/b +C`

Definite Integral

Consider the curve as shown. The area under the curve (the area bounded by the curve and the x-axis) can be found by dividing this area into infinitesimal areas and adding them up.

Consider this area to be divided into n parts, where each part can be assumed as a rectangle if n is very large. The length of each such part at `x=x_L` will be equal to `y_i = f(x_i)` while the breadth will be equal to `Delta x`
where `Delta x = (b-a)/n`

Area of each rectangle `= A_i = y_i Delta x`

The total area will be the sum of all these areas and will be given by

`Asum_(i=1)^(i=n) y_i Delta x`

if `Delta x -> 0,` the same area is represented by `int_(x=a)^(x=b) y dx` or `int _(x=a)^(x=b) f(x) dx`

This integral is known as definite integral of the curve `y = f(x)` between `x = a` to `x = b`, where `a` and `b` are known as the lower and upper limits of the integral respectively.

Fundamental Theorem of Integral Calculus

If `intf(x)dx =F(x)+C, ` then `intf(x)dx= F(x)_a^b = F(b)-F(a)`

Application of Calculus in Kinematic

The problems in kinematics can be solved using the differential and integral calculus, in addition to the already known equations which are given as under

`V = (dx)/(dt) ;`

`a= (dv)/(dt) = (dv)/(dx) xx (dx)/(dt) = v (dv)/(dt) ; a= (dv)/(dt) = d/(dt)((dx)/(dt)) = (d^2x)/(dt^2)`

( Where 'x' is displacement, V is velocity and 'a' is acceleration at time t)
Similarly, for circular motion

`omega =(d theta)/(dt)`

`alpha = (d omega)/(dt) = (d omega)/(d theta) xx (d theta)/(dt) = (omega d omega)/(d theta)` or `alpha =(d omega)/(dt) = d/(dt)(d theta)/(dt) = (d^2 theta)/(dt^2)`

( Where `theta` is angular displacement, `omega` is angular velocity and `alpha` is angular acceleration at time t)

Also by the definition of integral

`Delta x = int vdt , Delta v = int a dt`

`Delta theta = int omega dt , Delta omega = int alpha dt`

NOTE :

`(dx)/(dt)` is called as instantaneous velocity, it is the velocity in small time dt. Average velocity over a period of time `Delta t` can be given as `v = (Delta x)/(Delta t)`