Physics PROJECTILE MOTION
Please Wait... While Loading Full Video

PROJECTILE MOTION

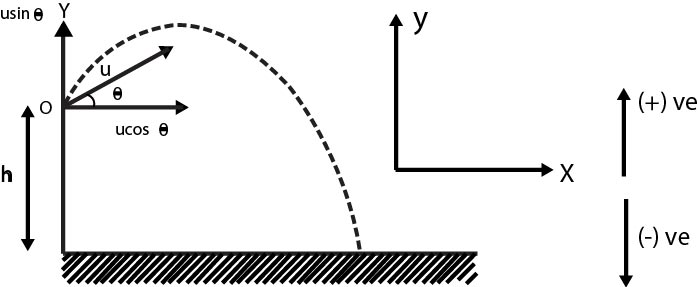
Basic concept

(I) Any particle which is thrown into space or air such
that it moves under the influence of an external force
(e.g. gravity, electric forces etc.) is called a projectile.
The motion of such a particle is referred to as
projectile motion.

(ll) It is an example of two dimensional motion with
constant acceleration.

(III) If the force acting on the projectile is constant,
then acceleration is constant. When the force is in
oblique direction with the direction of initial velocity,
the resultant path is parabolic.

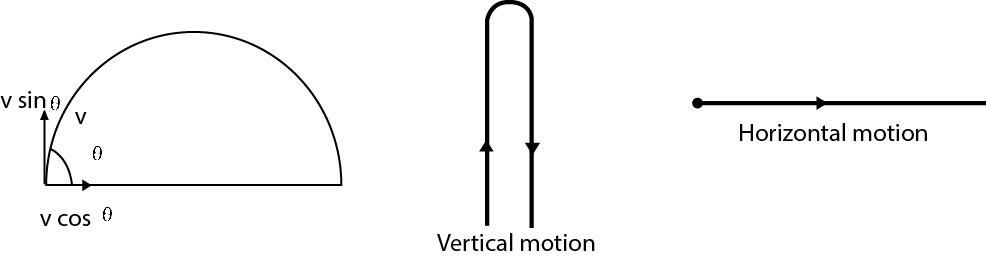
Parabolic motion = vertical motion + horizontal
motion

(IV) Projectile motion can be considered to be two
simultaneous motions in mutually perpendicular
directions which are completely independent of each
other i.e. horizontal motion and vertical motion.

Ground to ground projectile

Consider a projectile thrown from horizontal ground
with a velocity u making an angle q with the
horizontal. Take the point of projection as origin O
and the path of the projectile in the first quadrant of
`xy` - plane, as shown in the figure. The initial velocity
u is resolved in the horizontal and vertical directions
i.e.

`u_x = u cos theta, u_y = u sin theta`

Since gravity is the only force acting on the projectile
in vertically downward direction, (ignoring air
resistance)

`a_x =0 , a_y =-g`

Analyzing the motion of the projectile in horizontal and vertical directions:

Horizontal direction Vertical di rection

`(a)` Initial velocity `u_x= u cos theta`
(a) Initial velocity `u_y = u sin theta`

`(b)` Acceleration `a_x = 0 (b)` Acceleration `a_y =-g`

`(c)` Velocity after time `t`, `v_x = u cos theta`
(c) Velocity after
time `t` , `vy = u sin theta-g t`

The position vector of the projectile after time `t` is

`vecr = xhati+yhatj= (u cos theta.t)hati +(u sin theta -1/2 g t^2)hatj`

`vecv = v_xhati+v_yhatj = (u cos theta)hati +(u sin theta -g t)hatj` Velocity after time `t` is

Acceleration is consant, `veca = a_xhati+a_yhatj = =- g hatj`

Trajectory equation:

The path traced by the
projectile is called the trajectory of the projectile.

For displacement in the horizontal direction, `x = u_x .t`

`x = u cos theta .t................(1)`

For displacement in the vertical direction,

`y = u_y .t -1/2 g t^2`

`y = u sin theta .t -1/2 g t^2.....................(2)`

Substituting the value oft from eqn. (1) into eqn. (2),
we get

`y = u sin theta . x/(u cos theta) -1/2 g. (x/(u cos theta))^2`

`=> y = x tan theta -(gx^2)/(2u^2 cos^2 theta) => y= x tan theta[1-x/R]`
( R is the horizontal range covered by the projectile)

The equation of trajectory of the projectile is that of a
parabola because the projectile covers a parabolic path.

Time of flight:

The displacement along vertical
direction is zero for grow1d to ground projectile

`(u sin theta)T -1/2 g T^2 =0` `[T = (2 u sin theta)/g]`

Horizontal range :

The horizontal displacement of
the projectile from the point of projection to the point
it strikes the ground is called the horizontal range of
the projectile.

`R = u_x .T`

`R = u cos theta . (2 u sin theta)/g`

`R = (u^2 sin 2 theta)/g`

Maximum height :

Applying `v^2 =u^2 +2as` in the vertical direction between
the point of projection and the topmost point. we get

`0^2 = u^2 sin^2 theta - 2gH`

`H = (u^2 sin^2 theta)/(2g)`

Resultant velocity, at any Instant t

`vecv = v_xhati +v_yhatj = u cos theta hati +(u sin theta -g t)hatj`

`|vec v| = sqrt(u^2 cos^2 theta +(u sin theta - g t)^2)` & `tan alpha = v_y/v_x = (u sin theta - g t)/(u cos theta)`

`alpha` is the angle made by the velocity vector of the
projectile with the horizontal at any time instant `t` .

General result :

(1) For maximum range `q = 45- R_(max) = u^2/g`

In this situation `H_(max) = (u^2 sin^2 45 )/(2g) = u^2/(4g),`

`H_(max) = R_(max)/4`


(2) We get the same range for two angles of projection
a and (90 -a ).But in each of the two cases, maximum
height attained by the particle is different.

`R = (2 u^2 sin alpha cos alpha)/g = (2 u^2 sin(90- alpha)cos(90- alpha))/g`

(3) If `R = H` i.e, `(u^2 sin 2 theta)/g = (u^2 sin^2 theta)/(2g) ,`

`(2 u^2 sin theta cos theta)/g = (u^2 sin ^2 theta)/(2g)`

`tan q =4 ; q = tan -14`

(4)Range can also be exposed as

`R = (u^2 sin 2 theta)/g =(2 u sin theta . u cos theta)/g = (2u_xu_y)/g`

Change In momentum

(1) Initial velocity `vecu_i = u cos theta hati + u sin theta hat j`

(2) Final velocoity `vecu_f = u cos theta hati - u sin theta hat j`

Change in velocity from the point of projection to the
point where the projectile strikes the ground.

`Delta vecu = vecu_f- vecu_i = -2u sin theta hatj`

(3) Change in momenmm from the point of
projection to the point where the projectile strikes the
ground.

`Delta vecP = vecP_f -vecP_i =m(vecu_f- vecu_i ) =m(-2 u sin theta)hatj = -m2u sin theta hat j ,`

where m is the mass of the projectile

(4) Velocity at the highest point of the projectile is
`u cos theta hat i` . Change in momentum from the point of
projection to the highest point `= -m u sin theta hatj`

Projectile thrown horizontally from an eleva ted point

Consider a projectile thrown from point 0 at some
height h from the ground with a velocity u, in the
horizontal direction.

Analyzing the projectile motion along the horizontal
and vertical directions.


Horizontal direction Vertical direction

(i) Initial velocity `u_x= u` (i) Initial velocity `u_y= 0`

(ii) Acceleration `a_x= 0` (ii) Acceleration `a_y =- g`


`text(Trajectory Equation:)`

The path traced by the
projectile is called the trajectory.

After time `t` , `x = ut.............(1)`

`y = -1/2 g t^2.....................(2)`

From eqn. `(1)` `t= x/u`

Put value oft in eqn. `(2) y = -1/2 g(x/u)^2, y = -(gx^2)/(2u^2)`

This Is the equation of trajecto


`text(Velocity at a general point P(x, y))` after time t

Here horizontal velocity of the projectile after time `t` ,
`vx = u`

Velocity of projectile in vertical direction after time `t`

`v_y = 0-g t = -g t`

`vec v = v_x hati +v_y hatj = u_hati -g t hatj`

`text(Displacement)`
The displacement of the partide after
time `t` . Is expressed by

`S = xhati +y hatj `, where `x= ut, y = -1/2 g t^2,` `[s = uthati -1/2 g t^2hatj]`


`text(Time of flight)`
Time taken by the projectile to strike
the ground, is the time of night.
Apply `S = ut + 1/2at^2` , along vertical direction
`u = 0` in vertical direction, `y =-h`

`-h = -1/2 g t^2 , t = sqrt(2h/g)`

`text(Horizontal range)`
Distance covered by the projectile
along the horizontal direction between the point of
projection to the point where it strikes the ground.

`R = u_x t = u sqrt((2h)/g)`

Projectile fired from the top of a tower in upward inclined direction

Consider a projectile thrown from point oat height h from
the ground with speed u at an angle ewith the horizontal
in the upward direction.

Horizontal direction Vertical direction

(i) Initial velocity `u_x = ucos theta` (i) Initial velocity `u_y = u sin theta`

(ii) Acceleration `a_x =0` (ii) Acceleration `a_y=-g`

`text(Equation of trajectory)`

`y = u sin theta t -1/2 g t^2..................(1)`

`x = u cos theta xx t ......................(2)`

Eliminating t between (1) & (2)

`y = x tan theta - (gx^2)/(2 u^2cos^2 theta)`



`text(Velocity at any time t)`

At any time `t`
`V_x = ucos theta ,V_y= usin theta -g t`
`vecV-=V_xhati+v_yhatj = ucos theta hati +(usin theta -g t)hatj`


`text(Displacement at any lime t)`

At any time t

`y = u sin theta t -1/2 g t^2 , x= u cos theta t`

`vecS = x hati + y hatj = (u cos theta)hati +(u sin theta t -1/2 g t^2)hatj`


`text(Time of flight)`

`y = u sin theta t -1/2 g t^2 ` (for displacement in vertical direction)

`y = -h, -h= u sin theta t -1/2 g t^2`

Solving the above quadratic and accepting the positive
value oft, we get the time of flight.


Horizontal range -
Distance covered by projectile
along horizontal direction between point of
projection and the point where it strikes the ground.

`R = u_xt = u cos theta xx text(time of flight)`
 
SiteLock