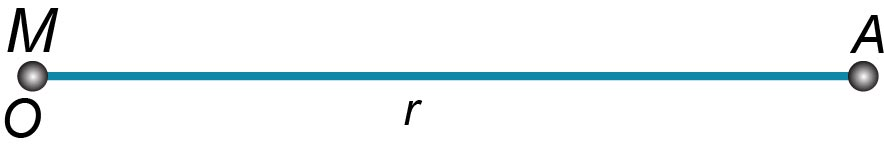Physics GRAVITATION

Gravitational Potential :

At a point in a gravitational field, potential `( v )` is defined as the work done by the external agent against the gravitational field in bringing unit mass from infinity to that point.

Mathematically, `V = W/m`

`=>` By the definition energy, `U = W ` So `V = U/m, ` i.e; `U = mV`

Thus, gravitational potential at a point represents potential energy of a unit point mass at that point.

`=> ` by definition of work `intvecF_(ext).vec(dr)`

But, `vecF_(ext) = - vecF_(gravitation)`

`W = -intF_(gravitation). vec(dr)`

So, `V = (intvecF_(gravitation) . vec(dr))/m = - intvecE. vec (dr)`

`[(vecF_(gravitation))/m = vecE]`

i.e, `dV = - E dr` or `E = -(dV)/(dr)........................(1)`

So the potential can also be defined as a scalar function of position whose negative gradient i.e., space derivative gives field intensity.

`=>` Negative of the slope of `V` vs `r` graph gives intensity.

Let `V` and `E` denotes the gravitational potential and gravitational field at point. Is it possible to have

`text((a))` `V = 0, E ne 0`
`text((b))` `V ne 0 , E = 0`
`text((c))` `V = 0, E = 0`
`text((d))` `V ne 0, E ne 0`

`text(Calculation of Gravitational Potential :)`

`text((a))` `text(Gravitational potential at a point due to a point mass)`
`text((b))` `text(Gravitational potential at a point due to a ring)`
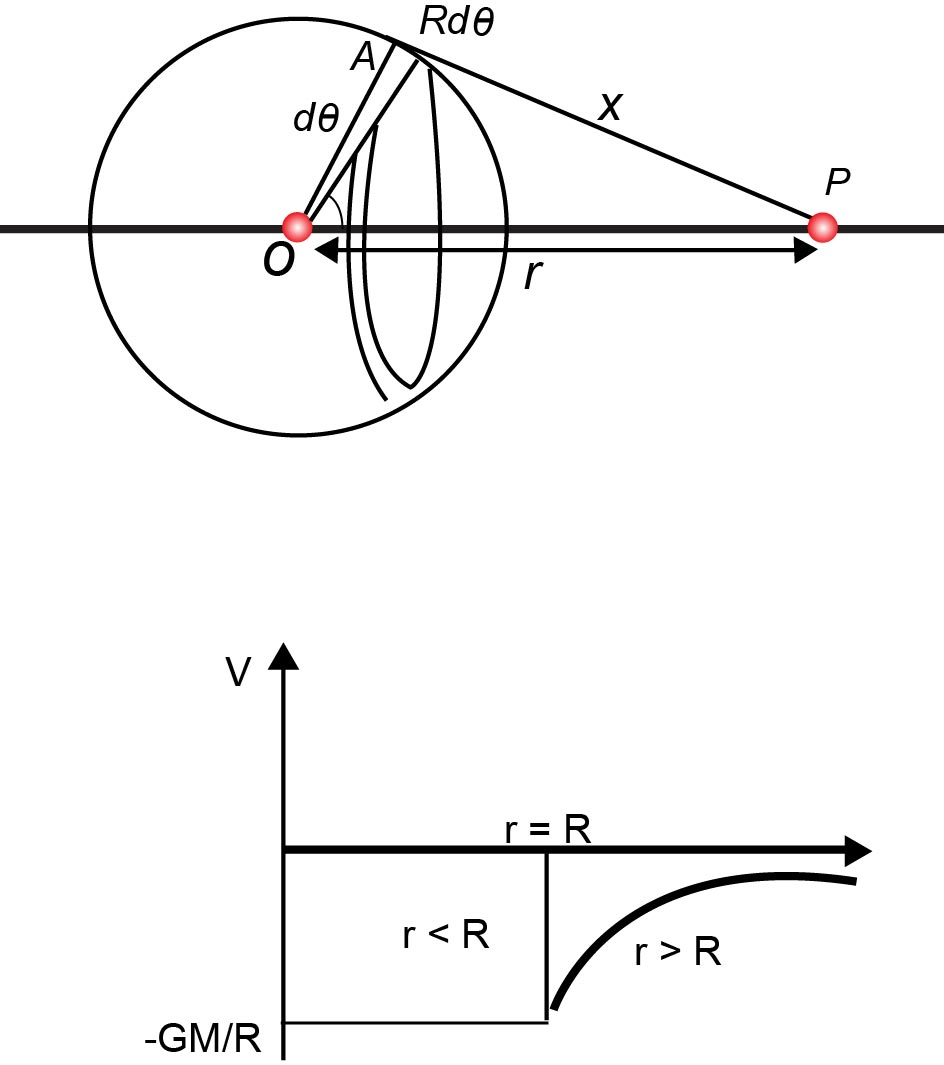
`text((c))` `text(Gravitational potential at a point due to a spherical shell (hollow sphere))`
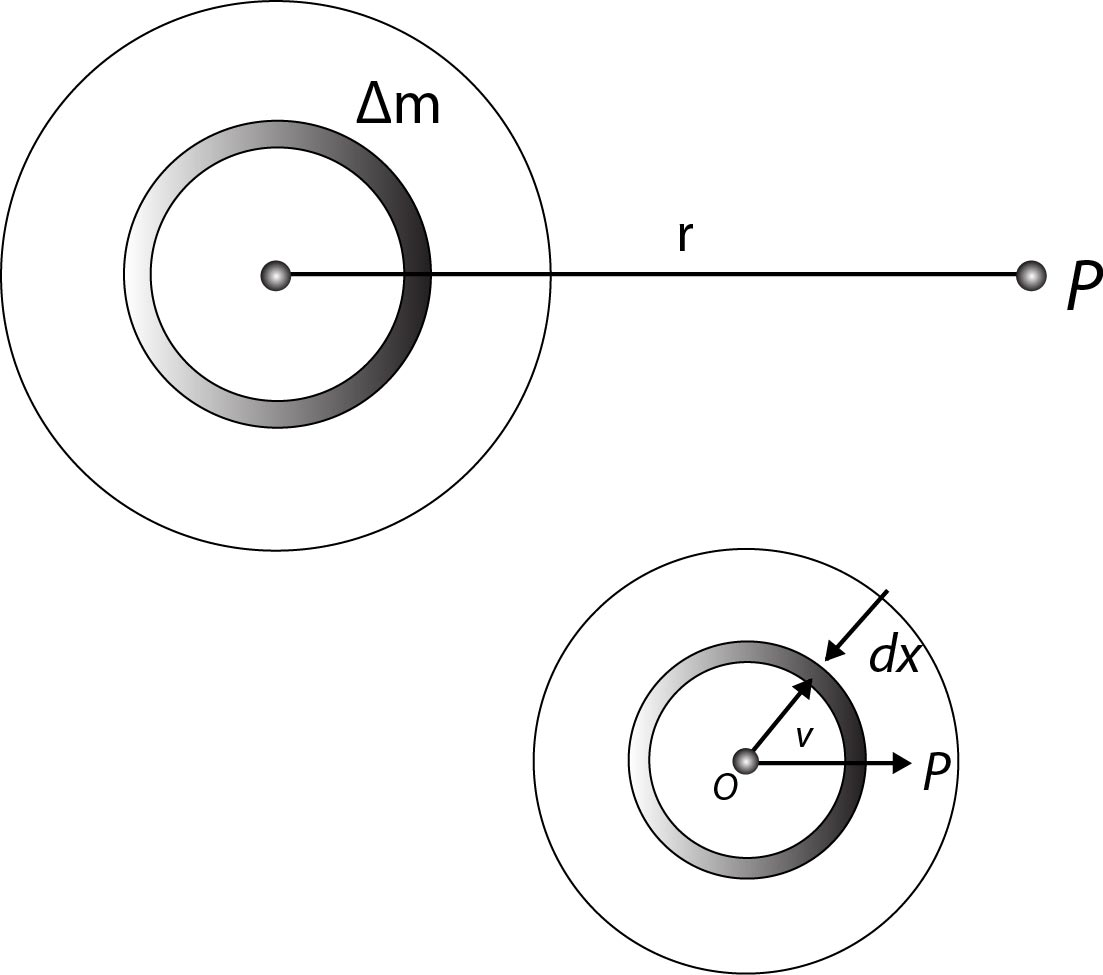
`text((d)) text(Gravitational potential due to a homogeneous solid sphere)`

`text(Gravitational potential at a point due to a point mass)`

We have, gravitational field due to a point mass

`E = (GM)/r^2`

[The negative sign in used as gravitational force is attractive]

`therefore` `V = - int EDdr = - (GM)/r +C` when , `r = oo, V = 0` So `C = 0`

`therefore` `V = - (GM)/r .................(2)`

`text(Gravitational potential at a point due to a ring)`

Let `M` be the mass and `R` be the radius of a thin ring.

Considering a small element of the ring and treating it as a point mass, the potential at the point `P` is

`dV = - (Gdm)/Z = - (Gdm)/sqrt(R^2 +r^2)`

Hence, the total potential at the point P is given by

`V =- int(Gdm)/sqrt(R^2 + r^2) =- (GM)/sqrt(R^2 +r^2).................(3)`

At `r=0, (dV)/(dr) =0` gravitational field is zero at the centre.

`text(Gravitational potential at a point due to a spherical shell (hollow sphere))`

Consider a spherical shell of mass `M` and radius `R` . Pis a point at a distance 'r' from the centre `O` of the shell.

Consider a ring at right angles to `OP` . Let `theta` be the angular position of the ring.
The radius of the ring `R sin theta ;` The width of the ring `= R d theta`

The surface area of the ring `= (2 pi R sin theta) . R d theta`

`=2 pi R^2 sin theta d theta`

The mass of the ring `= (2 pi R^2 sin theta d theta) xx M/(4 pi R^2)`

`=(M sin theta d theta)/2`

If `'x '` is the distance of the point `P` from a point on the ring, then the potential at `P` due to the ring.

`dV = -(GM sin theta d theta)/(2x)`

From the 'cosine-property' of the triangle `OAP ,x^2 = R^2 + r^ 2 -2 R r cos theta`

Differentiating,
`2 x dx = 2R r sin theta d theta`

` sin theta d theta = (x dx)/(Rr)`

Substituting the value of `sin theta d theta ,` we get

`dV = -(GM)/(2x) xx (x dx)/(Rr) =- (GM)/(2Rr) dx`

`text(Case I :)`

When the point P lies outside the shell.

`V = - (GM)/(2Rr) int_(r-R)^(r+R)dx = - (GM)/(2Rr) [x]_(r-R)^(r+R)`

`V = -(GM)/(2Rr) [(r+R)-(r-R)]`

`V = - (GM)/r....................(4)`

This is the potential at `P` due to a point mass Mat `O` .

For external point, a spherical shell behaves as a point mass supposed to be placed at its center.

`text(Case II)`

When the point P lies inside the spherical shell.

`V = - (GM)/(2Rr) int_(R - r)^(R+r) dx = - (GM)/(2 R r) [x]_(R-r)^(R+r)` or `V = - (GM)/R....................(5)`

This expression is independent of `r` . Thus, the potential at every point inside the spherical shell is of constant magnitude and it is equal to the potential on the surface of the shell.

Thus, the gravitational field inside a spherical shell is zero everywhere.

Graphical representation of the variation of `V` with `r` in case of a hollow spherical shell as shown in fig.

`text(Gravitational potential due to a homogeneous solid sphere)`

`text(Case-I)`

When the point `P` lies outside the sphere.

Consider a homogeneous solid sphere of mass `M` and radius `'R'` , `P` is a point at a distance `'r'` from the center of the sphere.

The solid sphere may be supposed to be made up of large number of thin concentric spherical shells. Consider one such shell of mass `Delta m` .

The potential at P due to the shell `= - (G Deltam)/r`

So, the potential at P due to the entire sphere.

`V = sum (G Delta m)/r = - G/r sum Delta m,`

`V = - (GM)/r`.......................(6) `[M = sum Delta m]`

Hence for an external point a solid sphere behaves as if the whole of its mass is concentrated at the centre.

`text(Case II)`

When the point `P` lies inside the sphere.

Let us consider a concentric spherical surface through the point `P` . The potential at `P` arises due to the inner sphere and the outer thick spherical shell.

`V = V_1 +V_2,`
where `V_1 =` potential due to the inner sphere and `V_2 =` potential due to the outer thick shell .

The mass of the inner sphere `= (4 pi r^3)/3 rho,` where

`rho =` density of sphere `= M/(4/3 pi R^3) = (3M)/(4 pi R^3)`

The potential at `P` due to this sphere

`V_1 = - (G[(4 pi r^3)/3] rho)/r = - (4 pi G rho)/3 r^2.....................(7)`

To find `V_2` , consider a thin concentric shell of radius `x` and thickness `dx` .

The volume of the shell `= 4pi x^2 dx`

The mass of the shell `= 4 pi x^2 dx rho`

The potential at P due to this shell

`V_2 = - int_r^R 4 pi G rho x dx = - 4 pi G rho[x^2/2]_r^R = -4 pi G rho[R^2/2 -r^2/2]`

`= - 2 pi G rho[R^2-r^2]`

`V_1 +V_2 = -(4 pi G rho r^2)/3 - 2 pi G rho [R^2 - r^2]`

`=(4 pi G rho)/3[r^2 + (3R^2)/2 - (3r^2)/2] = - (4 pi G rho)/3[(3R^2)/2 - (3r^2)/2]`

`=(4 pi G )/3 *(3M)/(4 pi R^3)[(3R^2 -r^2)/2]`

or `V = (GM)/(2R^3)[3R^2 - r^2].........................(8)`

at `r =0,` `(dv)/(dr) = 0`

Hence gravitational field is zero at the centre of a solid sphere.