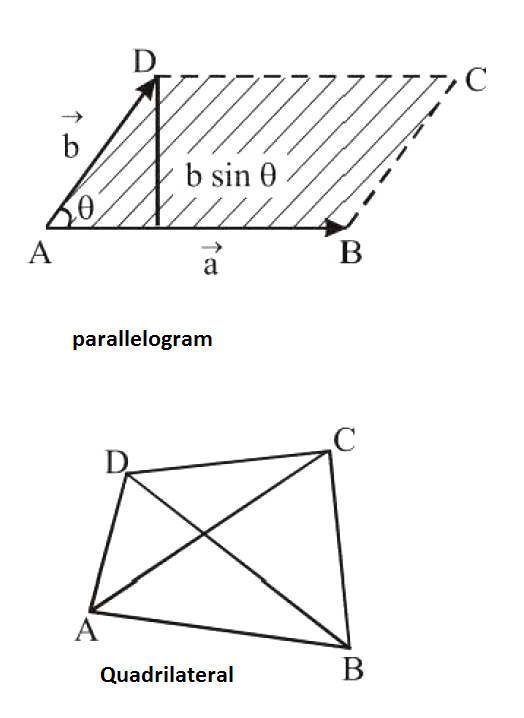
Area of a triangle :
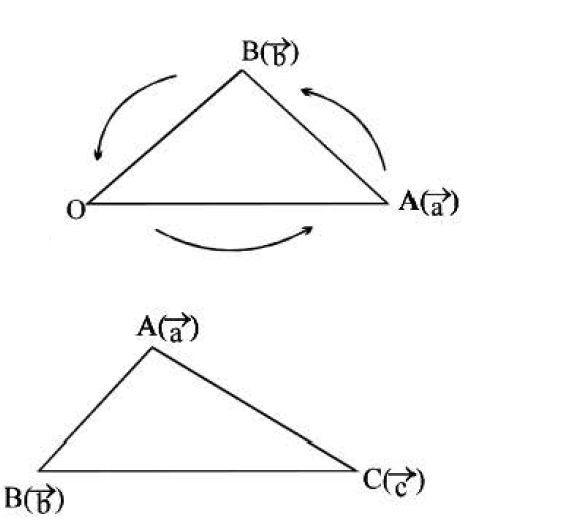
1. Area of triangle `ABC =1/2 ab sin theta =1/2 |vec(a)xxvec(b) | =1/2 |vec(AB)xxvec(AC) |`
2. If `vec(a) ,vec(b),vec(c)` are position vectors of vertices of a `Delta ABC` then its
Area `= 1/2 |(vec(a)xxvec(b)) +(vec(b)xxvec(c)) +(vec(c)*vec(a)) |`
Note:
`(i)` lf 3 points with position vectors `vec(a) ,vec(b)` and `vec(c)` are collinear then `vec(a) xx vec(b) + vec(b) xx vec(c)+ vec(c) xx vec(a)=0`
`(ii)` Unit vector perpendicular to the plane of the `Delta ABC` when `vec(a),vec(b),vec(c)` are the p.v. of its angular point is
` hat(n) = pm ( vec(a) xx vec(b) + vec(b) xx vec(c) + vec(c) xx vec(a) )/(2Delta)` ,where `vec(a),vec(b),vec(c)` are the position vectors of the angular points of the triangle `ABC` .
2. If `vec(a) ,vec(b),vec(c)` are position vectors of vertices of a `Delta ABC` then its
Area `= 1/2 |(vec(a)xxvec(b)) +(vec(b)xxvec(c)) +(vec(c)*vec(a)) |`
Note:
`(i)` lf 3 points with position vectors `vec(a) ,vec(b)` and `vec(c)` are collinear then `vec(a) xx vec(b) + vec(b) xx vec(c)+ vec(c) xx vec(a)=0`
`(ii)` Unit vector perpendicular to the plane of the `Delta ABC` when `vec(a),vec(b),vec(c)` are the p.v. of its angular point is
` hat(n) = pm ( vec(a) xx vec(b) + vec(b) xx vec(c) + vec(c) xx vec(a) )/(2Delta)` ,where `vec(a),vec(b),vec(c)` are the position vectors of the angular points of the triangle `ABC` .