Theory of Interference
Consider a homogeneous medium in which there are two point sources of sinusoidal spherical waves, `S_1` and `S_2` with the same period T. Let `E_1` and `E_2` be the optical disturbances arriving from the two sources at a point P. These disturbances can be written as
`E_1 =A_1 sin(omegat)`
`E_2 = A_2 sin (omegat + phi)`
Let the amplitudes `A_1` and `A_2` depend on the strengths of the sources and on the distance of the sources from P. From principle of superposition the resultant optical disturbance at P is a sinusoidal function of angular frequency `omega` and amplitude A given by
`A^2 = A_1^2 + A_2^2+ 2A_1 A_2 cosphi..........(1)` (from superposition)
We know that `IpropA^2`. Hence, the distribution of light intensity in the region of space surrounding the sources is given by:
`I=I_1 + I_2 + 2sqrt(I_1I_2) cos phi.........(2)`
Intensity will be maximum when `cosphi = 1`
`therefore` `I_(max)=(sqrtI_1 + sqrtI_2)^2`
Intensity will be minimum when `cosphi = -1`
`therefore` `I_(mi n)=(sqrtI_1 - sqrtI_2)^2`
Where `I_1` and `I_2` are the intensities observed when one or the other source is present alone and `I` is the intensity observed when both sources are present simultaneously. We see that the resultant intensity `I` is greater or smaller than the sum of the two separate intensities, `I_1 + I_2`, depending on whether the third term on the right side of equation is positive or negative. This term represents the effect of interference. Intensity maxima are found at points where the two waves are in phase; and minima are found at points where two waves are out of phase. Thus, interference phenomena have a considerable effect on the local distribution of light intensity in the space surrounding the source. They do not, however, change the space average of the intensity, which remains equal to the space average of `I_1 + I_2` as is required by the principle of conservation of energy. We see immediately that this is true when we note that the average value over space of the third term in equation (2) is zero.
Now question arises; how these maxima and minima occur?
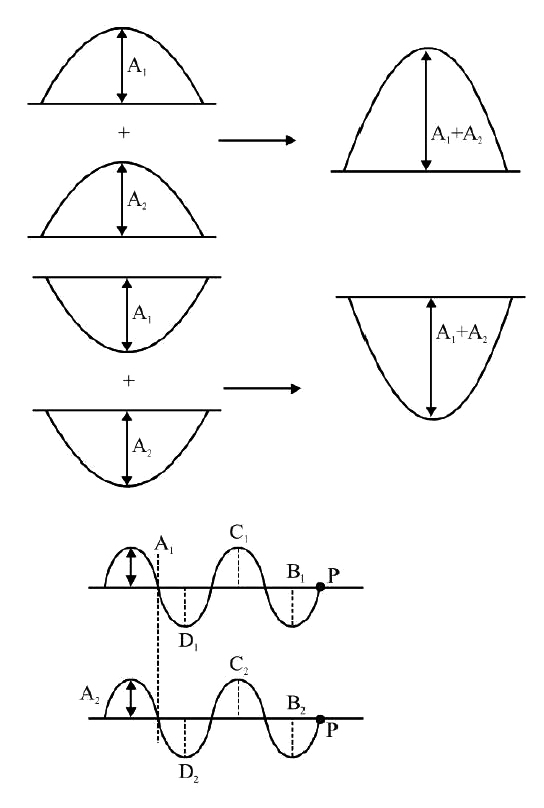
Intensity maxima occurs where amplitudes of two interfering waves add to give the maximum value. i.e. when maximum positive value, of one wave appears simultaneously with the maximum positive value of the other. or the negative extreme of one coincides with negative extreme of the other wave. To obtain a maxima at a point continuously fora long rime, we must obtain the wave at that point in same phase i.e. the crest must always appear with crest, and trough with lengths are same, as shown in figure.
At point P, a continuous maxima will appear if `B_1` and `B_2` reach there simultaneously, also `C_1, C_2` and `D_1, D_2` must follow same. As the velocity of light depends only on the medium and is therefore same for both waves; the above condition can be achieved only if
`B_1 P= B_2 P`
`C_1 P = C_2 P`
i.e. `lamda_1=lamda_2`
`=>` `lamda_1=c/f_1` and `lamda_2=c/f_2`
`therefore` `f_1=f_2`
Such waves for which frequency is same are called coherent waves and corresponding sources are coherent sources.
`E_1 =A_1 sin(omegat)`
`E_2 = A_2 sin (omegat + phi)`
Let the amplitudes `A_1` and `A_2` depend on the strengths of the sources and on the distance of the sources from P. From principle of superposition the resultant optical disturbance at P is a sinusoidal function of angular frequency `omega` and amplitude A given by
`A^2 = A_1^2 + A_2^2+ 2A_1 A_2 cosphi..........(1)` (from superposition)
We know that `IpropA^2`. Hence, the distribution of light intensity in the region of space surrounding the sources is given by:
`I=I_1 + I_2 + 2sqrt(I_1I_2) cos phi.........(2)`
Intensity will be maximum when `cosphi = 1`
`therefore` `I_(max)=(sqrtI_1 + sqrtI_2)^2`
Intensity will be minimum when `cosphi = -1`
`therefore` `I_(mi n)=(sqrtI_1 - sqrtI_2)^2`
Where `I_1` and `I_2` are the intensities observed when one or the other source is present alone and `I` is the intensity observed when both sources are present simultaneously. We see that the resultant intensity `I` is greater or smaller than the sum of the two separate intensities, `I_1 + I_2`, depending on whether the third term on the right side of equation is positive or negative. This term represents the effect of interference. Intensity maxima are found at points where the two waves are in phase; and minima are found at points where two waves are out of phase. Thus, interference phenomena have a considerable effect on the local distribution of light intensity in the space surrounding the source. They do not, however, change the space average of the intensity, which remains equal to the space average of `I_1 + I_2` as is required by the principle of conservation of energy. We see immediately that this is true when we note that the average value over space of the third term in equation (2) is zero.
Now question arises; how these maxima and minima occur?
Intensity maxima occurs where amplitudes of two interfering waves add to give the maximum value. i.e. when maximum positive value, of one wave appears simultaneously with the maximum positive value of the other. or the negative extreme of one coincides with negative extreme of the other wave. To obtain a maxima at a point continuously fora long rime, we must obtain the wave at that point in same phase i.e. the crest must always appear with crest, and trough with lengths are same, as shown in figure.
At point P, a continuous maxima will appear if `B_1` and `B_2` reach there simultaneously, also `C_1, C_2` and `D_1, D_2` must follow same. As the velocity of light depends only on the medium and is therefore same for both waves; the above condition can be achieved only if
`B_1 P= B_2 P`
`C_1 P = C_2 P`
i.e. `lamda_1=lamda_2`
`=>` `lamda_1=c/f_1` and `lamda_2=c/f_2`
`therefore` `f_1=f_2`
Such waves for which frequency is same are called coherent waves and corresponding sources are coherent sources.