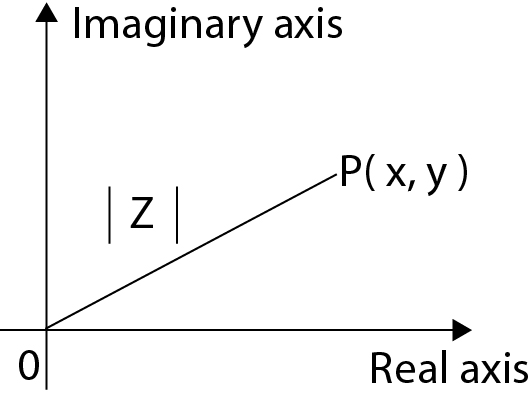Angle `(theta)` made by the line segment joining the point on the complex plane representing the complex number `z` to the origin from the positive real axis is called argument of complex number `z` which is denoted as `arg(z) = theta`.

`text(General Argument :)`
If `OP` makes an angle `theta ` with real axis then `theta` is called one of the argument of `z.`General values of argument of `z` are given by `2npi + theta`, `n in I.` Note that any two argument of the same complex number `z` differ by `2pi`.
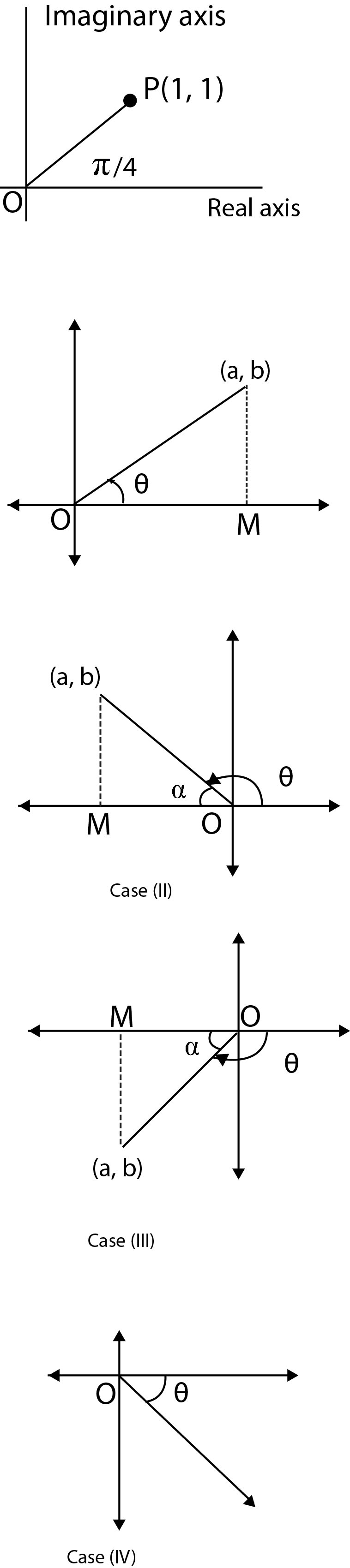
`e.g.` if `z=1+i` then `arg(z)=pi/4`
`therefore` General value of argument of `z=2npi+pi/4, n in I`

`text(Note that)` by specifying the modulus and argument, a complex number is completely defined. However for the complex number `0 + 0 i` the argument is not defined and this is the only complex number which is completely defined by talking in terms of its modulus. i.e.,` |z |= 0.`

`text(Principal value of argument :)`
The unique value of `theta` such that `-pi < theta<= pi` is called principal value of argument. Unless otherwise stated, `amp z` refers to the principal value of argument.

`text(Working rule for finding principal argument of Complex number)` `Z`
Let `Z=a+ib`

First compute `alpha=tan^-1(|b|/|a|)`

`text(Case) (I) :` If `z` lies in `I` quadrant i.e. `a, b > 0` then `amp (z) = theta = alpha`.


`text(Case) (II) :` If `z` lies in `II` quadrant i.e. `a<0, b > 0` then `amp (z) = theta =(pi- alpha)`.

`text(Case) (III) :` If `z` lies in `III` quadrant i.e. `a<0, b < 0` then `amp (z) = theta =-(pi- alpha)`.


`text(Case) (IV) :` If `z` lies in `IV` quadrant i.e. `a>0, b < 0` then `amp (z) = theta =- alpha`.



`text(Properties of Arguments)`

`(i) arg(z_1z_2) = arg(z_1) + arg(z_2) + 2kpi, k in I`

In general , arg `(z_1,z_2,z_3........z_n)`

`=arg(z_1) + arg(z_2) + arg(z_3)+ ..............+ agr(z_n) + 2kpi , k in I`

`(ii) arg(z_1/z_2) = arg(z_1) - arg(z_2) + 2k pi, k in I`

where, proper value of k must be chosen, so that RHS lies in `(-pi,pi)` .

`(v) ` If `arg(z_2/z_1) = theta.` then `arg(z_1/z_2) = 2npi - theta , ` where `n in I`

`(vi) arg(barz) = - arg(z)`


`text(Note :)`

`(i)` If `z` is purely real positive complex number then `amp(z) = 0.`

`(ii)` If `z` is purely imaginary positive complex number then `amp(z) =pi/2.`

`(iii) arg(z/z) = 2arg(z) + 2kpi , k in I`

`(iv) arg(z^n) = n , arg (z) + 2kpi , k in I`

`(iii)` If `z` is purely real negative complex number then `amp(z) = pi.`

`(iv)` If `z` is purely imaginary negative complex number then `amp(z)= -pi/2`.

`text(Least positive argument :)`

The value of `theta` such that `0 < theta<=2 pi` is called the least positive argument.

`(i) |z_1 + z_2| = |z_1| + |z_2| ⇔arg(z_1) = arg(z_2) `

`(ii) |z_1 + z_2|= |z_1|-|z_2| ⇔ arg(z_1) - arg(z_2) = pi`

Proof (i) Let `arg(z_1) = theta` and `arg(z_2) = phi`

`therefore` `|z_1+ z_2|= |z_1|+ |z_2|`

On squaring both sides, we get

`|z_1 + z_2|^2 = |z_1|^2 + |z_2|^2 + 2 |z_1||z_2|`

`=> |z_1|^2 + |z_2|^2 + 2|z_1||z_2| cos (theta- phi) = |z_1|^2 + |z_2|^2 + 2 |z_1||z_2|`

`=> cos (theta- phi) = 1 `

`therefore` `theta - phi =0` or `theta= phi`

`therefore` `arg(z_1) = arg(z_2)`

`(ii) ∵|z_1+z_2| = |z_1|-|z_2|`

On squaring both sides, we get

`|z_1+z_2|^2 = |z_1^2|+|z_2|^2-2|z_1| |z_2|`

`=> |z_1|^2 + |z_2|^2 + 2|z_1||z_2| cos (theta- phi) = |z_1|^2 + |z_2|^2 - 2 |z_1||z_2|`

`=> cos (theta- phi) = -1 `

`therefore` `theta- phi = pi`

or `arg(z_1)- arg(z_2) = pi`


`text(Points to consider)`

`1. |z_1-z_2|= |z_1|+|z_2| ⇔arg(z_1)= arg(z_2)`

`2. |z_1-z_2|= |z_1|- |z_2| ⇔ arg(z_1) - arg(z_2) = pi`

`3. |z_1-z_2| = |z_1+z_2| ⇔ arg(z_1) -= arg(z_2) = pm pi/2 , barz_1 , z_2` and `z_1/z_2` are purely imaginary.