Composite Function
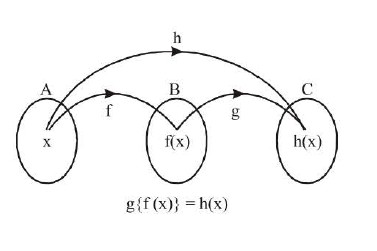
Let `f: A-> B` & `g: B -> C` be two functions. Then the fun ction `gof: A-> C` defined by
`(got) (x) ~ g(f(x)) AA x in A`
is called the composite ofthe two functions `f` & `g`. Diagramatically
`overset x (->) f overset (f(x)) (->) g -> g (f(x))`
Thus the image of every `x in A` under the function `gof` is the `g`- image of the `f`- image of `x`.
Note that gof is defined only if `AA x in A, f(x)` is an element of the domain of `g` so that we can take its `g`- image. Hence for `gof` of two functions `f` & `g`, the range off must be a subset of the domain of `g`.
`(got) (x) ~ g(f(x)) AA x in A`
is called the composite ofthe two functions `f` & `g`. Diagramatically
`overset x (->) f overset (f(x)) (->) g -> g (f(x))`
Thus the image of every `x in A` under the function `gof` is the `g`- image of the `f`- image of `x`.
Note that gof is defined only if `AA x in A, f(x)` is an element of the domain of `g` so that we can take its `g`- image. Hence for `gof` of two functions `f` & `g`, the range off must be a subset of the domain of `g`.