Inverse of a Function
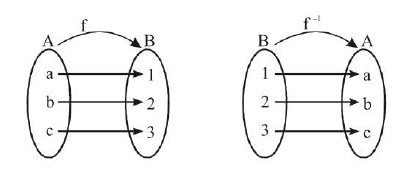
Let `f: A-> B` be a one- one & onto function, then their exists a unique function
`g: B-> A` such that `f(x) = y Leftrightarrow g(y) = x, AA x in A` & `y in B`. Then `g` is said to be inverse off.
Thus `g = f^-1: B-> A = {(f(x), x) I (x, f(x)) in f}`.
Consider a one-one onto function with domain `A= {a, b, c}` & range `B = {I , 2, 3}`
Domain of `f= {a, b, c} =` Range of `f^-1`
Range of `f = {1 , 2, 3} =` Domain of `f^- 1`
Note:
(a) Only one-one onto functions (i.e., Bijections) are invertible.
(b) To find the inverse
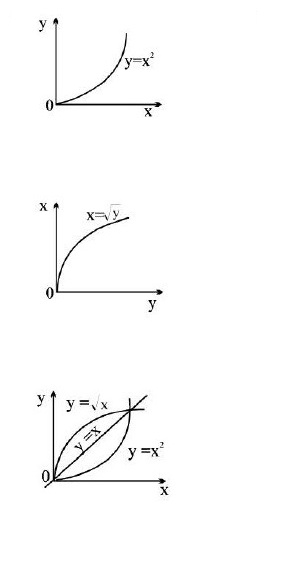
Step-1 : write `y = f(x)`
Step-2: solve this equation for `x` in terms of `y` (if possible)
Step-3: To express `f^-1` as a function of `x`, interchange `x` and `y`.
`g: B-> A` such that `f(x) = y Leftrightarrow g(y) = x, AA x in A` & `y in B`. Then `g` is said to be inverse off.
Thus `g = f^-1: B-> A = {(f(x), x) I (x, f(x)) in f}`.
Consider a one-one onto function with domain `A= {a, b, c}` & range `B = {I , 2, 3}`
Domain of `f= {a, b, c} =` Range of `f^-1`
Range of `f = {1 , 2, 3} =` Domain of `f^- 1`
Note:
(a) Only one-one onto functions (i.e., Bijections) are invertible.
(b) To find the inverse
Step-1 : write `y = f(x)`
Step-2: solve this equation for `x` in terms of `y` (if possible)
Step-3: To express `f^-1` as a function of `x`, interchange `x` and `y`.