Mathematics ONE-ONE AND ONTO FUNCTION

One-One Function (Injective mapping)

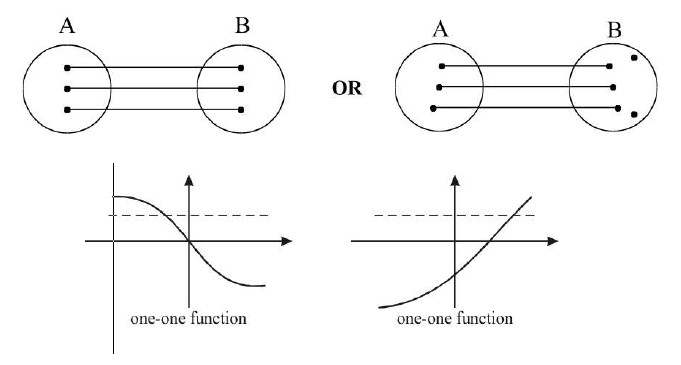
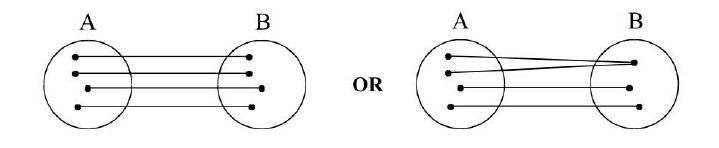
A function `f: A-> B` is said to be a one-one function or injective mapping if different elements of `A` have different `f` images in `B`. Thus for `x_1 x_2 in A` & `f(x_1), f(x_2) in B`,

`f(x_1) = f(x_2) <=> x_1 = x_2` or `x_1 != x_2 <=> f(x_1) != f(x_2)`.

Examples: `R ->R f(x) = x^3 + 1 ; f(x) = e^-x; f(x) = lnx`

Remember that a linear function is always one-one.

Diagramatically an injective mapping can be shown as in Fig

Note:
(i) A continuous function which is always increasing or decreasing in whole domain, then `f(x)` is one-one.

(ii) A function is one to one if and only if a horizontal line intersects its graph at most once.

Onto function (Surjective mapping)

If the function `f: A-> B` is such that each element in `B` (co-domain) is the fimage of at least one element in `A`, then we say that fisa function of `A` 'onto' `B`.

Thus `f: A-> B` is surjective iff `AA b in B, 3` some `a in A` such that `f(a) = b`.

`f: R->R f(x) = 2x + 1;\ \ \ \ \ \ f:R-> R^+\ \ \ \ f(x) = e^x; f:R^+ -> R f(x) = lnx`

Diagramatically surjective mapping can be shown as

Note that: If range = co- domain, then `f(x)` is onto. Any polynomial of degree odd , `f: R-> R` is onto.

Many-one function (not injective)

A function `f: A->B` is said to be a many one function if two or more elements of `A` have the same `f ` image in `B`. Thus `f: A-> B` is many one if for;

`x_1 ,x_2 in A , f(x_1) = f(x_2)` but `x_1 != x_2`.

Examples : `R -> R f(x) = [ x] ; f(x) =| x |; f(x) = ax^2 + bx + c ; f(x) = sin x`

Diagramatically a many one mapping can be shown as Fig 1

Note :

(i) Any continuous function which has atleast one local maximum or local minimum in its domain, then f(x)is many- one.ln other words, if a line parallel to x- axis cuts the graph of the function atleast at two
points, then fis many- one.

(ii) I fa function is one- one, it cannot be many- one and vice versa.
One One + Many One = Total number of mappings.

Into function:

If `f: A-> B` is such that there exists atleast one element in co-domain which is not the image of any element in domain, then `f(x)` is into.

e.g. `f: R-> R \ \ \ \ \ \ f(x) = [x]. |x |. sgnx, f(x) = ax^2+bx+c`

Diagramatically into function can be shown as Fig 2

Note:

(i) If a function is onto, it cannot be into and vice versa. A polynomial of degree even define from `R -> R` will always be into & a polynomial of degree odd defined from `R-> R` will always be onto.

(ii) A function can be one of these four types:

(a) one- one onto (injective & surjective) `(I nn S)`

(b) one-one into (injective but not surjective) `(I nn barS)`

(c) many- one onto (surjective but not injective) `(S nn barI)`

(d) many- one into (neither surjective nor injective ) `(I nn S)`