A function `f` is called an algebraic function if it can be constructed using algebraic operations such as addition, substraction, multiplication, division and taking roots, started with polynomials.

e.g. `f(x) = sqrt(x^2+1) ; g(x) = (x^4 -16x^2)/(x+sqrtx) + (x-2) xx root (x+1) (3)`

Note:

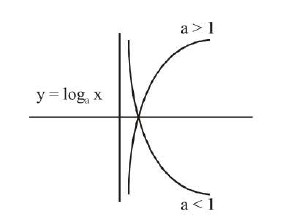
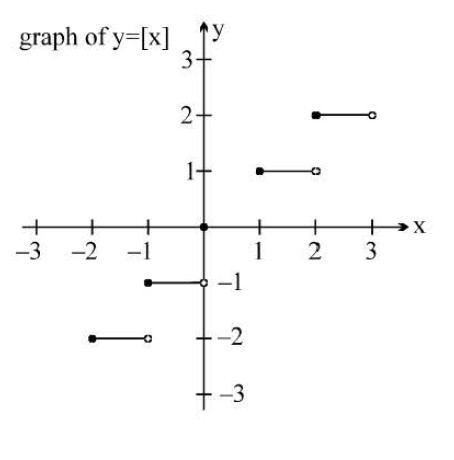
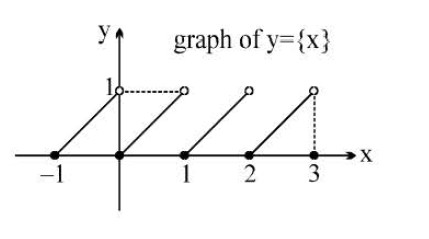
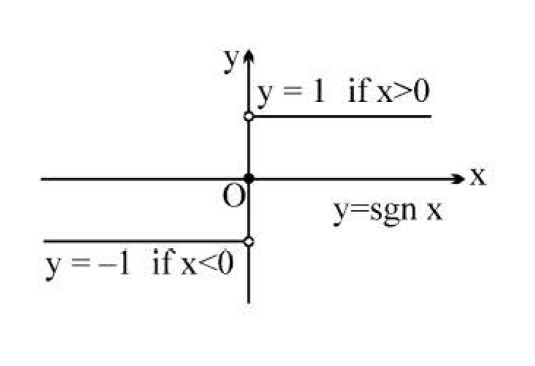All polynomial are algebraic but converse is not true. Functions which are not algebraic, are known as Transcidential function.

A rational function is a function of the form `y = f(x) = (g(x))/(h(x))`, where where `g(x)` & `h (x)` are polynomials & `h(x) !=0`. The domain of `f(x)` is set of real `x` such that `h (x) != 0`.

e.g `f(x) =(2x^4 -x^2 +1)/(x^2 -4); D = {x|x!=pm 2}`

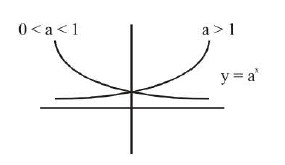
A function `f(x) = a^x = e^(xlna) (a > O , a!=1, , x in R)` is called an exponential function. `f(x) = a^x` is called an exponential function
because the variable xis the exponent. It should not be confused with power function. `g (x) = x^2` in which variable xis the base.

For `f(x) = e^x ` domain is `R` and range is `R^+`.

For `f(x) = e^(1/x)` domain is `R- {0}` and range is `R^+ - {1}. i.e (0,1) uu(1,oo)`

`f(x) = 1/(ln x)` with domain `R^+ -{1}`, range is `R- {0}`

A function of the form `y = log,x, x > 0, a > 0, a!= 1`, is called Logarithmic function.

`

A function `y = f(x) = | x | ` is called the absolute value function or Modulus function. It is defined as:

`y =|x| = {tt((x, if ,x >=0),(-x, if, x < 0))`

For `f(x) =|x|`, domain is `R` and range is `R^+ uu {0}`.

For `f(x) =1/(|x|)` or `(|x|)/x^2` , domain is `R - {0}` and range is `R^+`. .

A function `y= f(x) =Sgn(x)` is defined as follows:

`y = f(x) = {tt((1, text(for), x > 0),(0,text(for),x=0),(-1,text(for),x < 0))`

It is also written as Sgn `x = |x|/ x` or `x/|x|`

`x!=0; f(0)=0`

Note:

`Sgn (Sgnx) = Sgn x;`

`y =Sgn(x^2-1) ={tt((1, |x| > 1),(0, |x| =1),(-1, |x| < 1))`

₹

The function `y= f(x) = [x]` is called the greatest integer function where `[x]` denotes the greatest integer less than or equal to `x` . Note that for :

`-1 <= x <= 0 ; [x] =-1 \ \ \ \ 0 <= x < 1 ; [x] =0`

`1 <= x < 2 : [x] =1 \ \ \ \ 2<= x < 3 ; [x] =2` and so on.

For `f(x) = [x]`, domain is ` R` and range is `1`.

For `f(x) = 1/[x]` , domain is `R- [0,1)` and range is `{1/n| n in I-{0}}`

Properties of greatest integer function

(a) `[x] <= x < [x] + 1` and

`x-1 < [x] <= x , 0 <= x -[x] <1`

(b) `[x+m] = [x] + m`, if `m` is an integer.

(c) `[x] + [y] <= [x + y] <= [x]+[y]+1`

(d) `[x] +[x] = {tt(( 0, text(if x is an integer )),(-1, text(otherwise)))`

(e) `[x] >= n => x in [n,oo) AA n in I`

(f) `[x] > n => x in [n+1,o) AA n in I`

(g) `[x] <= n => x in (-oo,n+1) AA in I`

(h) `[x] < n => x in (-oo,n) AA n in I`

It is defined as :

`g(x) = {x} = x - [x]`.

e.g. the fractional part of the number `2.1` is

`2.1 - 2 = 0.1` and the fractional part of- 3.7 is 0.3. The period of this function is `1` and graph of this function is as shown.

For `f(x) = {x}` , domain is `R` and range is `[0, 1)`

For `f(x) =1/{x}`, domain is `R - I`, range is `( 1 , oo)`

Properties of fractional part:

(a) `0 <= {x} < 1`

(b) `{x + n} = {x}, n in I`

(c) {x} +{-x} `= {tt((0, x in I),(1, x != I))`

The function `f : A->A` defined by `f(x) = x AA x in A` is called the identity of `A` and is denoted by `I_A`.

It is easy to observe that identity function defined on `R` is a bijection.

`f:R->R, \ \ \ \ \ \ f(x) =x`

A function `f: A -> B` is said to be a constant function if every element of `A` has the same `f` image in `B`.Thus `f: A->B; f(x) = c , AA x in A `, `c in B` is a constant function. Note that the range of a constant function is a singleton and a constant function may be one- one or many- one, onto or into.

e.g. `f(x) = [ {x} ]; g(x) = sin^2x + cos^2x; h (x) = sgn(x^2 - 3x + 4)` etc, all are constant functions.