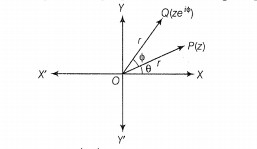
Argand Plane
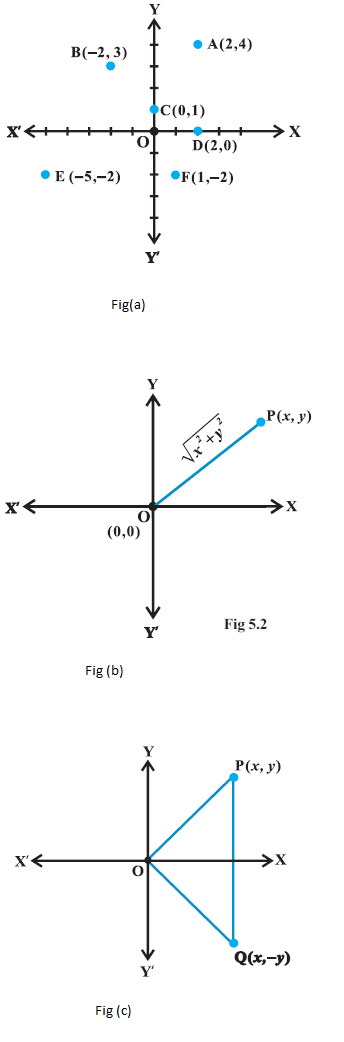
We already know that corresponding to each ordered pair of real numbers `(x, y),` we get a unique point in the `XY`-plane and vice-versa with reference to a set of mutually perpendicular lines known as the `x`-axis and the `y`-axis. The complex number `x + iy` which corresponds to the ordered pair `(x, y)` can be represented geometrically as the unique point `P(x, y)` in the `XY`-plane and vice-versa. Some complex numbers such as `2 + 4i, - 2 + 3i, 0 + 1i, 2 + 0i, - 5 -2i` and `1 - 2i` which correspond to the ordered pairs `(2, 4), ( - 2, 3), (0, 1), (2, 0), ( -5, -2),` and `(1, - 2),` respectively, have been represented geometrically by the points `A, B, C, D, E,` and `F,` respectively in the Fig `(a)`.
`text(The plane having a complex number assigned to each of its point is called the complex plane or the Argand plane.)`
Obviously, in the Argand plane, the modulus of the complex number `x + iy = sqrt(x^2 + y^2)` is the distance between the point `P(x, y)` to the origin `O (0, 0)` `(Fig b).` The points on the `x`-axis corresponds to the complex numbers of the form `a + i 0` and the points on the `y`-axis corresponds to the complex numbers of the form `0 + i b.` The `x`-axis and `y`-axis in the Argand plane are called, respectively, the real axis and the imaginary axis.
The representation of a complex number `z = x + iy` and its conjugate `z = x - iy` in the Argand plane are, respectively, the points `P (x, y)` and `Q (x, - y).` Geometrically, the point `(x, - y)` is the mirror image of the point `(x, y)` on the real axis `(Fig c).`
`text(The plane having a complex number assigned to each of its point is called the complex plane or the Argand plane.)`
Obviously, in the Argand plane, the modulus of the complex number `x + iy = sqrt(x^2 + y^2)` is the distance between the point `P(x, y)` to the origin `O (0, 0)` `(Fig b).` The points on the `x`-axis corresponds to the complex numbers of the form `a + i 0` and the points on the `y`-axis corresponds to the complex numbers of the form `0 + i b.` The `x`-axis and `y`-axis in the Argand plane are called, respectively, the real axis and the imaginary axis.
The representation of a complex number `z = x + iy` and its conjugate `z = x - iy` in the Argand plane are, respectively, the points `P (x, y)` and `Q (x, - y).` Geometrically, the point `(x, - y)` is the mirror image of the point `(x, y)` on the real axis `(Fig c).`