Physics MICROSCOPE

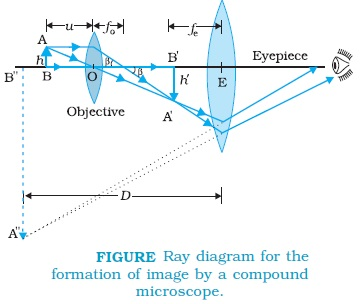
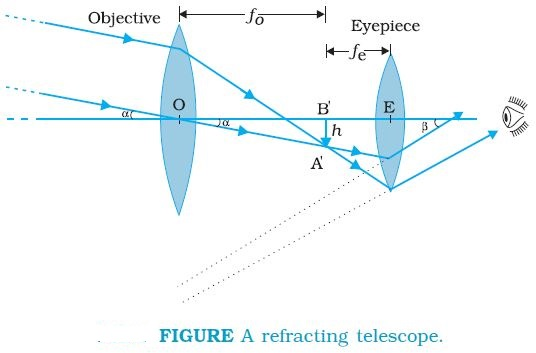
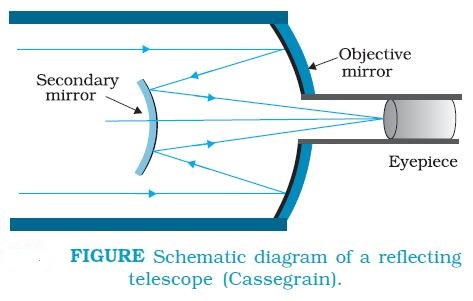
The Microscope

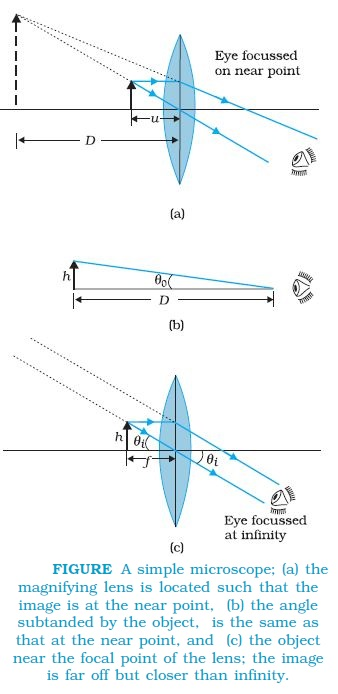
A simple magnifier or microscope is a converging lens of small focal length (Fig.). In order to use such a lens as a microscope, the lens is held near the object, one focal length away or less, and the eye is positioned close to the lens on the other side. The idea is to get an erect, magnified and virtual image of the object at a distance so that it can be viewed comfortably, i.e., at 25 cm or more. If the object is at a distance f, the image is at infinity. However, if the object is at a distance slightly less than the focal length of the lens, the image is virtual and closer than infinity. Although the closest comfortable distance for viewing the image is when it is at the near point (distance D ≅ 25 cm), it causes some strain on the eye. Therefore, the image formed at infinity is often considered most suitable for viewing by the relaxed eye. We show both cases, the first in Fig. (a), and the second in Fig. (b) and (c).

The linear magnification m, for the image formed at the near point D, by a simple microscope can be obtained by using the relation

`m=v/u=v(1/v -1/f)=(1-v/f)`

Now according to our sign convention, v is negative, and is equal in magnitude to D. Thus, the magnification is

`m= (1+D/f).......(1)`

Since D is about 25 cm, to have a magnification of six, one needs a convex lens of focal length, f = 5 cm.

Note that m = h′/h where h is the size of the object and h′ the size of the image. This is also the ratio of the angle subtended by the image to that subtended by the object, if placed at D for comfortable viewing. (Note that this is not the angle actually subtended by the object at the eye, which is h/u.) What a single-lens simple magnifier achieves is that it allows the object to be brought closer to the eye than D.

`text(Angular Magnification :)`

We will now find the magnification when the image is at infinity. In this case we will have to obtained the angular magnification. Suppose the object has a height h. The maximum angle it can subtend, and be clearly visible (without a lens), is when it is at the near point, i.e., a distance D. The angle subtended is then given by

`tantheta_o = h/Dapproxtheta_(o)........(2)`

We now find the angle subtended at the eye by the image when the object is at u. From the relations

`(h^')/h=m=v/u`

we have the angle subtended by the image

`tantheta_i =(h^')/(-v)=h/(-v)*v/u = h/(-u) approx theta` The angle subtended by the object, when it is at u = �f.

`theta_i = h/f............(3)`

as is clear from Fig. (c). The angular magnification is, therefore

`m= (theta_i)/(theta_o) = D/f.......(4)`

This is one less than the magnification when the image is at the near point, Eq. (1), but the viewing is more comfortable and the difference in magnification is usually small.

Compound Microscope

A simple microscope has a limited maximum magnification (≤ 9) for realistic focal lengths. For much larger magnifications, one uses two lenses, one compounding the effect of the other. This is known as a compound microscope.

A schematic diagram of a compound microscope is shown in Fig. The lens nearest the object, called the objective, forms a real, inverted, magnified image of the object. This serves as the object for the second lens, the eyepiece, which functions essentially like a simple microscope or magnifier, produces the final image, which is enlarged and virtual. The first inverted image is thus near (at or within) the focal plane of the eyepiece, at a distance appropriate for final image formation at infinity, or a little closer for image formation at the near point. Clearly, the final image is inverted with respect to the original object. We now obtain the magnification due to a compound microscope. The ray diagram of Fig. shows that the (linear) magnification due to the objective, namely h′/h, equals

`m_(o)=(h^')/h=L/(f_o).......(5)`

where we have used the result

`tan beta=h/(f_o)=(h^')/L`

Here h′ is the size of the first image, the object size being h and `f_o` being the focal length of the objective. The first image is formed near the focal point of the eyepiece. The distance L, i.e., the distance between the second focal point of the objective and the first focal point of the eyepiece (focal length `f_e` ) is called the tube length of the compound microscope.

As the first inverted image is near the focal point of the eyepiece, we use the result from the discussion above for the simple microscope to obtain the (angular) magnification me due to it [Eq. (1)], when the final image is formed at the near point, is

`m_e=(1+D/f_e)......(6)`

When the final image is formed at infinity, the angular magnification due to the eyepiece is

`m_e=D/(f_e).....(7)`

Thus, the total magnification, when the image is formed at infinity, is

`m=m_o m_e=(L/f_o)(D/f_e)..........(8)`

Clearly, to achieve a large magnification of a small object (hence the name microscope), the objective and eyepiece should have small focal lengths.

Telescope

The telescope is used to provide angular magnification of distant objects (Fig.). It also has an objective and an eyepiece. But here, the objective has a large focal length and a much larger aperture than the eyepiece. Light from a distant object enters the objective and a real image is formed in the tube at its second focal point. The eyepiece magnifies this image producing a final inverted image. The magnifying power m is the ratio of the angle β subtended at the eye by the final image to the angle α which the object subtends at the lens or the eye. Hence

`mapprox=beta/alphaapproxh/(f_o)*(f_o)/h=(f_o)/(f_e).......(9)`

In this case, the length of the telescope tube is `(f_o)+(f_e)`

Terrestrial telescopes have, in addition, a pair of inverting lenses to make the final image erect. Refracting telescopes can be used both for terrestrial and astronomical observations.

Cassegrain Telescope

The main considerations with an astronomical telescope are its light gathering power and its resolution or resolving power. The former clearly depends on the area of the objective. With larger diameters, fainter objects can be observed. The resolving power, or the ability to observe two objects distinctly, which are in very nearly the same direction, also depends on the diameter of the objective. So, the desirable aim in optical telescopes is to make them with objective of large diameter. The largest lens objective in use has a diameter of 40 inch (~1.02 m). It is at the Yerkes Observatory in Wisconsin, USA. Such big lenses tend to be very heavy and therefore, difficult to make and support by their edges. Further, it is rather difficult and expensive to make such large sized lenses which form images that are free from any kind of chromatic aberration and distortions.

For these reasons, modern telescopes use a concave mirror rather than a lens for the objective. Telescopes with mirror objectives are called reflecting telescopes. They have several advantages. First, there is no chromatic aberration in a mirror. Second, if a parabolic reflecting surface is chosen, spherical aberration is also removed. Mechanical support is much less of a problem since a mirror weighs much less than a lens of equivalent optical quality, and can be supported over its entire back surface, not just over its rim. One obvious problem with a reflecting telescope is that the objective mirror focuses light inside the telescope tube. One must have an eyepiece and the observer right there, obstructing some light (depending on the size of the observer cage). This is what is done in the very large 200 inch (~5.08 m) diameters, Mt. Palomar telescope, California. The viewer sits near the focal point of the mirror, in a small cage. Another solution to the problem is to deflect the light being focused by another mirror. One such arrangement using a convex secondary mirror to focus the incident light, which now passes through a hole in the objective primary mirror, is shown the problem is to deflect the light being focused by another mirror. One such arrangement using a convex secondary mirror to focus the incident light, which now passes through a hole in the objective primary mirror, is shown in Fig. This is known as a Cassegrain telescope, after its inventor. It has the advantages of a large focal length in a short telescope.