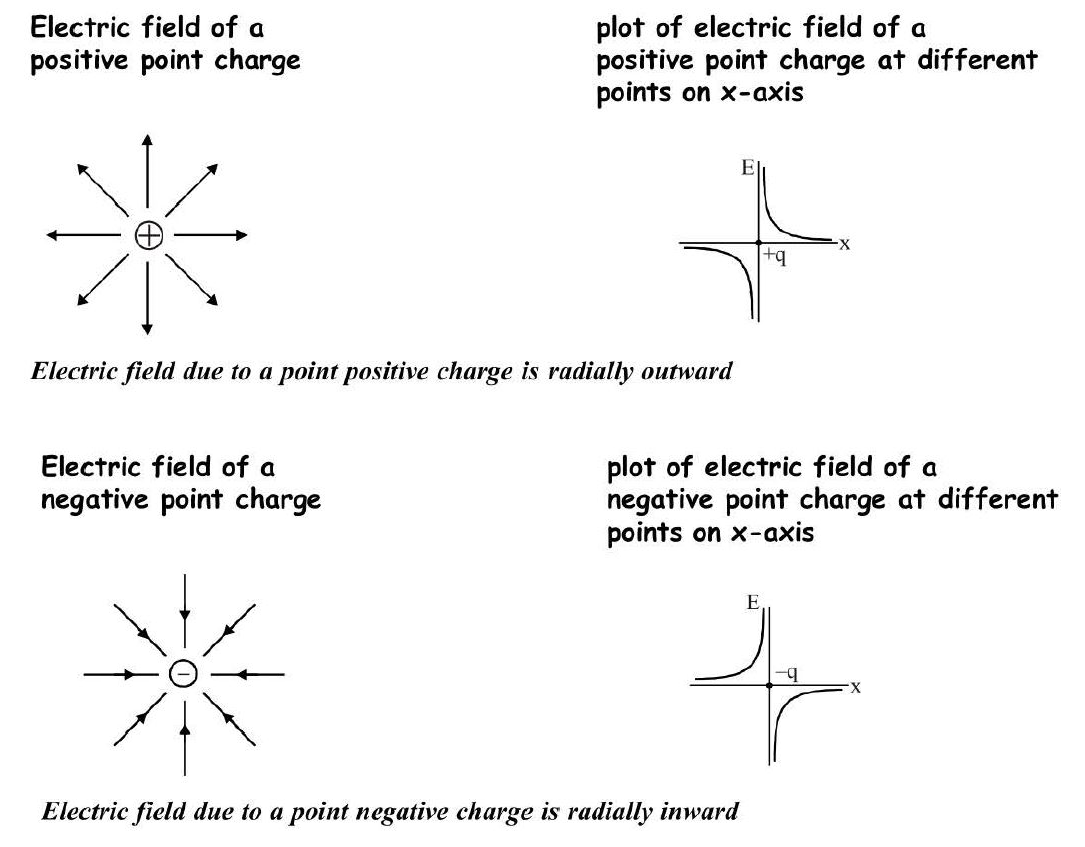
`text(Relationship between Electric Field and Electric Potential :)`
Place a charge q in electric field `vecE`.This field exerts a force `vecF = q vecE` on the charge .If you displace the charge by `dvecr` then field will do some work `dW = vecF.dvecr= qvecE.dvecr` on the charge. Change in electric potential energy during this displacement will be given by `dU = -qvecEdvecr`.
Therefore potential difference between initial and final point will be given by
`dV=-vecE.dvecr`
`text(Calculation of electric potential difference from electric field :)`
`dV=-vecE.dvecr`
`=>int_(V(vecr_1))^(V(vecr_2))dV=-int_(vecr)^(vecr_2)vecE.dvecr`
`=>V(vecr_2)-V(vecr_1)=intdV=-int_(vecr)^(vecr_2)vecE.dvecr`
In cartesian coordinate system
`dvecr=dxhati+dyhatj+dzhatk`
`=>vecE.dvecr=E_xdx+E_ydy+E_zdz`
`=>V(vecr_2)-V(vecr_1)=-int_(vecr)^(vecr_2)vecE.dvecr=-int_(x_1)^(x_2)E_xdx-int_(y_1)^(y_2)E_ydy-int_(z_1)^(z_2)E_zdz`
`text(Calculation of electric potential from electric field :)`
For our convenience we select potential of a point to be zero.This point is called reference point. Usually reference point is taken at infinity. In the above equation let us take `vecr=oo` and `vecr_2=vecr`, then the potential at a point can be written as
`V(vecr)=-int_oo^(vecr)vecEdvecr`
`text(Calculation of electric field from electric potential :)`
`dV=-vecEdvecr`
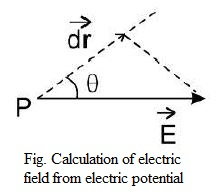
`dV=-(Ecostheta)dr`
`-(dV)/(dr)=Ecostheta`
(i.e. , Rate of decrease of potential)
Where `E costheta` is component of field in the direction of displacement. From the above expression.
Potential decreases maximum in the direction of field, `theta=0^@`.
It IS also clear that, `-(dV)/(dr)` is maximum in the direction of the field, so, we may conclude that, the electric potential decreases at maximum rate in the direction of the field.
The cartesian component of electric fie ld can be written as
`vecE=E_xhati+E_yhatj+E_zhatk`
and an infinitesimal displacement is `dvecr=dxhati+dyhatj+dzhatk`
Thus,
`dV=-vecEdvecr`
`=-[E_xdx+E_ydy+E_zdz]`
for a displacement in the x-direction,
dy = dz = 0 and so
`dV=-E_xdx`. Therefore,
`E_x=-((dv)/(dx))_text(y, z constant)`
A derivative in which all variables except one are held constant is called partial derivative and is written with `del` instead of `d`. The electric field is, therefore,
`E_x=-(delV)/(delx)`
`E_y=-(delV)/(dely)`
`E_z=-(delV)/(delz)`
i.e., if scalar potential function is given field can be calculated taking help ofthe above relations as
`vecE=-[(delV)/(delx)hati+(delV)/(dely)hatj+(delV)/(delz)hatk]`
`|vecE|=sqrt[((delV)/(delx))^2+((delV)/(delx))^2+((delV)/(delz))^2]`
`text(Relationship between Electric Field and Electric Potential :)`
Place a charge q in electric field `vecE`.This field exerts a force `vecF = q vecE` on the charge .If you displace the charge by `dvecr` then field will do some work `dW = vecF.dvecr= qvecE.dvecr` on the charge. Change in electric potential energy during this displacement will be given by `dU = -qvecEdvecr`.
Therefore potential difference between initial and final point will be given by
`dV=-vecE.dvecr`
`text(Calculation of electric potential difference from electric field :)`
`dV=-vecE.dvecr`
`=>int_(V(vecr_1))^(V(vecr_2))dV=-int_(vecr)^(vecr_2)vecE.dvecr`
`=>V(vecr_2)-V(vecr_1)=intdV=-int_(vecr)^(vecr_2)vecE.dvecr`
In cartesian coordinate system
`dvecr=dxhati+dyhatj+dzhatk`
`=>vecE.dvecr=E_xdx+E_ydy+E_zdz`
`=>V(vecr_2)-V(vecr_1)=-int_(vecr)^(vecr_2)vecE.dvecr=-int_(x_1)^(x_2)E_xdx-int_(y_1)^(y_2)E_ydy-int_(z_1)^(z_2)E_zdz`
`text(Calculation of electric potential from electric field :)`
For our convenience we select potential of a point to be zero.This point is called reference point. Usually reference point is taken at infinity. In the above equation let us take `vecr=oo` and `vecr_2=vecr`, then the potential at a point can be written as
`V(vecr)=-int_oo^(vecr)vecEdvecr`
`text(Calculation of electric field from electric potential :)`
`dV=-vecEdvecr`
`dV=-(Ecostheta)dr`
`-(dV)/(dr)=Ecostheta`
(i.e. , Rate of decrease of potential)
Where `E costheta` is component of field in the direction of displacement. From the above expression.
Potential decreases maximum in the direction of field, `theta=0^@`.
It IS also clear that, `-(dV)/(dr)` is maximum in the direction of the field, so, we may conclude that, the electric potential decreases at maximum rate in the direction of the field.
The cartesian component of electric fie ld can be written as
`vecE=E_xhati+E_yhatj+E_zhatk`
and an infinitesimal displacement is `dvecr=dxhati+dyhatj+dzhatk`
Thus,
`dV=-vecEdvecr`
`=-[E_xdx+E_ydy+E_zdz]`
for a displacement in the x-direction,
dy = dz = 0 and so
`dV=-E_xdx`. Therefore,
`E_x=-((dv)/(dx))_text(y, z constant)`
A derivative in which all variables except one are held constant is called partial derivative and is written with `del` instead of `d`. The electric field is, therefore,
`E_x=-(delV)/(delx)`
`E_y=-(delV)/(dely)`
`E_z=-(delV)/(delz)`
i.e., if scalar potential function is given field can be calculated taking help ofthe above relations as
`vecE=-[(delV)/(delx)hati+(delV)/(dely)hatj+(delV)/(delz)hatk]`
`|vecE|=sqrt[((delV)/(delx))^2+((delV)/(delx))^2+((delV)/(delz))^2]`