Conjuction(And)
Compound statement are combined by the word ` "and " ` (^) the resulting statement is called a conjunction denoted as `p` ^ `q`.
`e.g. `A point occupies a position and its location can be determined.
The component statement are
`\ \ \ \ \ \ \ \ p` : A point occupies a position
`\ \ \ \ \ \ \ \ q` : Its location can be determined
Both statements are true.
`text(Imp.:)` Do not think that a statement with ` "And"` is always a compound statement.
`e.g. `A mixture of alcohol and water can be separated by chemical methods.
(Here ` " And" ` refers to two things).
`text(Note:)`
`(i)` The compound statement with `'And'` is true if all its component statements are true.
`(ii)` The compound statement with `'And'` is false if any of its component statements is false (this includes the case that some of its component statements are false or all of its component statements are false).
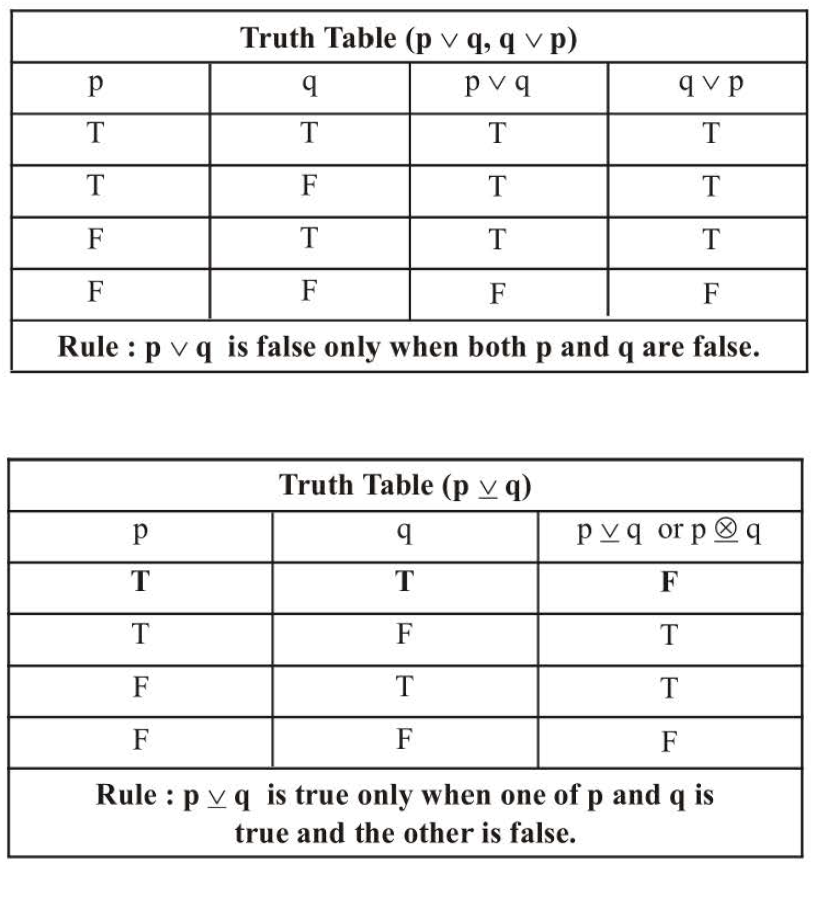
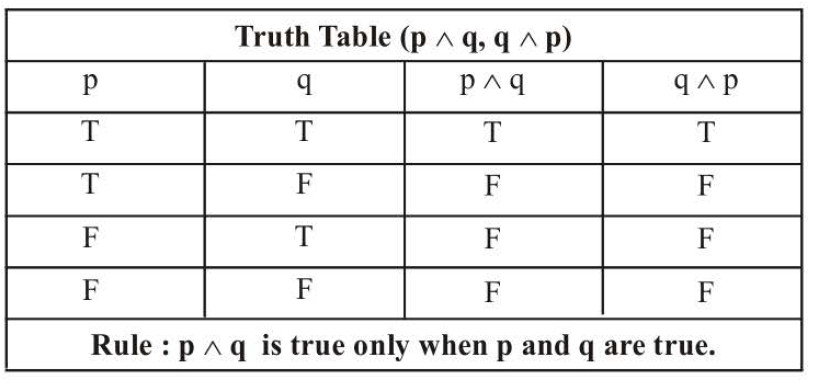
The following truth table shows the truth values of `p` ^ `q` (`p` and `q`) and `q ` ^ `p` ( `q` and `p`) .
`text(Remark :)` The above truth table shows that `p` ^ `q` = `q` ^ `p`.
`e.g. `A point occupies a position and its location can be determined.
The component statement are
`\ \ \ \ \ \ \ \ p` : A point occupies a position
`\ \ \ \ \ \ \ \ q` : Its location can be determined
Both statements are true.
`text(Imp.:)` Do not think that a statement with ` "And"` is always a compound statement.
`e.g. `A mixture of alcohol and water can be separated by chemical methods.
(Here ` " And" ` refers to two things).
`text(Note:)`
`(i)` The compound statement with `'And'` is true if all its component statements are true.
`(ii)` The compound statement with `'And'` is false if any of its component statements is false (this includes the case that some of its component statements are false or all of its component statements are false).
The following truth table shows the truth values of `p` ^ `q` (`p` and `q`) and `q ` ^ `p` ( `q` and `p`) .
`text(Remark :)` The above truth table shows that `p` ^ `q` = `q` ^ `p`.