Physics STANDING WAVES IN STRINGS AND ORGAN PIPES

Standing Wave

Standing wave is obtained due to superposition of two waves travelling with same speed in opposite directions along the same line.

Suppose two sine waves of equal amplitude and frequency propagate on a long string in opposite directions. The equations ofthe two waves are given by

`y_1 = Asin(omegat - kx)`
`y_2 = Asin(omegat + kx + phi)`

These waves interfere to produce what we can call standing waves.

To understand these waves, let us discuss the special case when `phi= 0`.

The resultant displacements of the particles of the string are given by the principle of superposition as

`y= y_1 + y_2`
`y=A[(omegat - kx)+(omegat + kx)]`
`y=2Asinomegatcoskx`
`y=(2Acoskx)sinomegat`

we may write, `y =A_0 sin (omegat)`
where `A_0=2Acoskx`

`text(The result obtained from the above equation are :)`

(a) As this equation satisfies the wave equation,

`(del^2y)/(delx^2)=1/v^2\(del^2y)/(delt^2)`

it represents a wave. However, as it is not of the form `f(ax - bt)`, the wave is not travelling and so is called standing or stationary wave or non- progressive wave.

(b) The amplitude of the resultant wave

`A_0 = 2A cos kx`

is not same for all prints of the medium but varies periodically with position (and not with time as in beats).

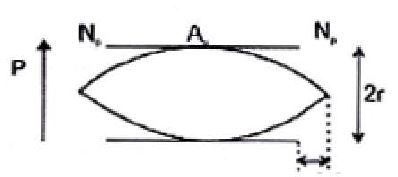
(c) The points for which amplitude is minimum are called nodes.

For nodes `coskx=0` i.e., `kx=pi/2,(3pi)/2,(5pi)/2....`

i.e., `x=lamda/4,(3lamda)/4,(5lamda)/4..........` [as `k=(2pi)/lamda`]

In a stationary wave, consecutive nodes are equally spaced and their separation is `lamda//2`.

(d) The points for which amplitude is maximum are called antinodes

For antinodes, `cos kx = - 1`

i.e., `kx=0,pi.2pi,3pi,.......`

`=>x=0,lamda/2,(2lamda)/2,(3lamda)/2,.....` [as `k=(2pi)/lamda`]

i.e., like nodes, antinodes are also equally spaced with spacing (`lamda//2`) and `A_(max)=- 2A`.
Furthermore, nodes and an tin odes are alternate with spacing (`lamda//4`).

(e) The nodes divide the medium into segments (or loops). All the particles in a segment vibrate in same phase, but in opposite phase with the particles in the adjacent segment. Twice in one period all the particles pass through their mean position simultaneously with maximum velocity (`Aomega`), the direction of motion being reversed after each half cycle. [see fig (a)]

(f) Standing waves can be transverse or longitudinal, e.g., in strings (under tension) if reflected wave exists, the waves are transverse-stationary, while in organ pipes waves are longitudinal stationary.

(g) As in stationary waves nodes are permanently at rest, so no energy can be transmitted across them, i.e, energy of one region (segment) is confined in that region. However, this energy oscillates between elastic potential energy and kinetic energy of the particles of the medium. When all the particles are at their extreme positions KE is minimum while elastic PE is maximum (as shown in figure A), and when all the particles (simultaneously) pass trough their mean position KE will be maximum while elastic PE minimum (Fig. B). The total energy confined in a segment (elastic PE + KE), always remains the same.

Standing Waves in String

`text(String fixed at both ends :)`
For a string fixed at both ends, the rigid end behaves as nodes. Suppose for a string of length L, one end is chosen as `x = 0` and the other end as `x = L`. In order that both ends are nodes, the length L must satisfy the condition,

`L=n(lamda/2)` ; for `n=1,2,3,....`

where n is number of loops formed.

`=>lamda=(2L)/n`

and corresponding frequencies are `f=v/lamda=n(v/(2L))` (v is the speed of the wave)

The set of frequencies given by the above equation are called natural frequencies or modes of oscillation of the system.

(a) When `n=1` i.e. when only one loop is formed `lamda= 2L`

and `f=v/(2L)=1/(2L)sqrt(T/mu)`

This is called fundamental frequency or (`f_0`) first harmonic.

(b) When `n = 2`

i.e. formed, `lamda= L`

and `f=2(v/(2L))=2f_0`

(c) When `n = 3`, `lamda=(2L)/3` and `f=3(v/(2L))=3f_0`

This is called third harmonic or second overtone.

Thus `n_(th)` harmonic or `(n - 1 )^(th)` overtone is given by

`f=nf_0=n(v/(2L))`

and `lamda=((2L)/3)`

Fundamental frequency of a string fixed at both ends is given

`f_0=v/(2L)=1/(2L)sqrt(T/mu)`

Where T is tension and `mu` is mass per unit length

Also `mu=` `text(Density x Area of cross-section)`

`text(String fixed at one end :)`
Standing waves can also be produced on a string which is fixed at one end whose other end is free to move in transverse direction. Such a free end can nearly be achieved by connecting the string to a very light thread.

Here we may take node at fixed end i.e. at `x = 0` and antinode at free end i.e. at `x = L`

`=>L=lamda/4,(3lamda)/4,(5lamda)/4......`

i.e., `L=(n-1/2)lamda/2` (Where `n = 1,2,3,......`)

`=>lamda=(4L)/(2n-1)`

Also `f=v/lamda=(2n-1)(v/(4L))`

Thus here fundamental frequency or first harmonic (forn `n=1`) is

`f_0=v/(4L)=1/(4L)sqrt(T/mu)`

and `lamda = 4L`

for `n = 2`

`f=(3v)/(4L)=3f_0`

and `lamda=(4L)/3`

Thus first overtone here is `3^(rd)` harmonic

For `n = 3`

`f=(5v)/(4L)=5f_0`

and `lamda=(4L)/5`

Thus second overtone here is fifty harmonic therefore in this case only odd harmonic are obtained.

Closed Organ Pipe

`A_P =` Pressure antinode
`A_S =` Displacement antinode
`N_P =` Pressure node
`N_S =` Displacement node.

`text(Fundamental mode :)`
The smallest frequency (largest wavelength) that satisfies the boundary condition for resonance (i.e. displacement node at left end and antinode at right end is `lamda_0 = 4l`, where `l =` length of closed pipe the corresponding frequency.

`nu_0=v/lamda=v/(4L)` is called the fundamental frequency `......(1)`

`text(First Overtone :)`
Here there is one node and one antinode apart from the nodes and antinodes at the ends.

`lamda_1=(4l)/3=(lamda_0)/3`

and corresponding frequency,

`nu_1=v/(lamda_1)=3nu_0`

This frequency is 3 rimes the fundamental frequency and hence is called the `3^(r d)` harmonic.

`n^(t h)` `text(Overtone :)`
In general, the `n^(th)` overtone will have n nodes and n antinodes between the two nodes at the ends. The corresponding wavelength is

`lamda_n=(4l)/(2n+1)=lamda/(2n+1)`

`=> nu_n=(2n+1)nu_0....(2)`

This corresponds to the `(2n + 1)^(th)` harmonic. Clearly only odd harmonic are allowed in a closed pipe.

Open Organ Pipe

`text(Fundamental mode :)`
The smallest frequency (largest wave length) that satisfies the boundary condition for resonance (i.e. displacement anrinodes at both ends) is,

`lamda_0=2l`

corresponding frequency, is called the fundamental frequency

`nu_0=v/(2l)`

`1^(st)` `text(Overtone :)` Here there is one displacement antinode between the two antinodes at the ends.

`lamda_1=l=(2l)/2=>lamda=(lamda_0)/2`

and corresponding frequency

`nu_1=v/(lamda_1)=2nu_0`

This frequency is 2 times the fundamental frequency and is called the 2nd harmonic.

`n^(th)` `text(Overtone :)` The `n^(th)` overtone has n displacement antinodes between the two antinode at the ends.

`lamda_n=(2l)/(n+1)=(lamda_0)/(n+1)`

and `nu_n=(n+1)nu_0`

This correspond to `(n + 1 )^(th)` harmonic, clearly both even and odd harmonics are allowed in an open pipe.

End Correction

The displacement antinode at an open end of an organ pipe lies slightly outside the open end. The distance of the antinode from the open end is called end correction and its value is given by

`e=0.6r`

where r = radius of the organ pipe.

With end correction, the fundamental frequency of a closed pipe (`f_c`) and an open orgon pipe (`f_o`) will be given by

`f_c=v/(4(l+0.6r))`

`f_0=v/(2(l+1.2r))`