Diffraction Due to a Single Slit (Width of Central Maximum)
The sketch shows the view from above a single slit. Let's assume that the slit is constant width and very tall compared with that width, so that we can consider the system as two-dimensional. With light at normal incidence, the pattern is symmetrical about the axis of the slit. On a distant screen, the light arriving on the axis from all points in the slit has travelled an equal distance from the slit, so the centre of the pattern is a maximum. The next question is what determines its width.
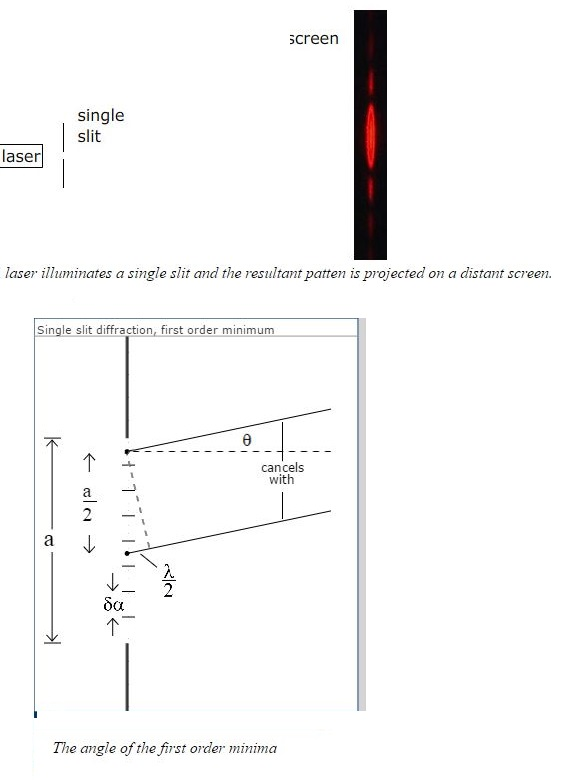
`text(First order minima :)`
The first minimum on either side of the central maximum. We call the slit width a, and we imagine it divided into two equal halves. Using the Huygens' construction, we consider a point at the very top of the slit, and another point a distance a/2 below it, i.e. a point at the very top of the lower half of the slit. Consider parallel rays from both points, at angle θ to the axis of symmetry.
The ray from the distance a/2 below has to travel an extra distance `((a sin θ)/2).` If this distance is half a wavelength, i.e. if
`a sin θ = λ`
then they are π/2 out of phase and they interfere destructively. Now, for every point in the top half of the slit, there is one in the bottom half a distance a/2 below and, at the angle that satisfies `asinθ = λ,` they all interfere destructively.
So the first minimum has `sin θ = λ/a.` On the other side of the axis of symmetry, `sin θ = -λ/a` is also a minimum. These two minima limit the broad central maximum.
`text(Higher order minima :)`
An argument like the one applies if, in our imagination, we divide the slit into any even number of equal slices. The diagram shows a division into four. Each half is divided into quarters, and light from a source in the first quarter cancels that from one in the second quarter. Similarly, sources in the third quarter are nullified by those in the fourth quarter. So this diagram represents the second order minima, where `sinθ = λ/(a/2),` or `sinθ = (2λ)/a.` For the nth order minima, we have
`asinθ = nλ `, where n is an integer, but not zero.
Remember that, on the axis where θ = 0, there is a minimum, so the minima are equally spaced in sin θ, except either side of the central maximum.
We can note too that, for light diffracting the throught slits, the slit is usually much wider than a wavelength, so the pattern is usually very small, so the approximation that sin θ = θ is usually good. Next we calculate how the intensity varies with sin θ.
`text(First order minima :)`
The first minimum on either side of the central maximum. We call the slit width a, and we imagine it divided into two equal halves. Using the Huygens' construction, we consider a point at the very top of the slit, and another point a distance a/2 below it, i.e. a point at the very top of the lower half of the slit. Consider parallel rays from both points, at angle θ to the axis of symmetry.
The ray from the distance a/2 below has to travel an extra distance `((a sin θ)/2).` If this distance is half a wavelength, i.e. if
`a sin θ = λ`
then they are π/2 out of phase and they interfere destructively. Now, for every point in the top half of the slit, there is one in the bottom half a distance a/2 below and, at the angle that satisfies `asinθ = λ,` they all interfere destructively.
So the first minimum has `sin θ = λ/a.` On the other side of the axis of symmetry, `sin θ = -λ/a` is also a minimum. These two minima limit the broad central maximum.
`text(Higher order minima :)`
An argument like the one applies if, in our imagination, we divide the slit into any even number of equal slices. The diagram shows a division into four. Each half is divided into quarters, and light from a source in the first quarter cancels that from one in the second quarter. Similarly, sources in the third quarter are nullified by those in the fourth quarter. So this diagram represents the second order minima, where `sinθ = λ/(a/2),` or `sinθ = (2λ)/a.` For the nth order minima, we have
`asinθ = nλ `, where n is an integer, but not zero.
Remember that, on the axis where θ = 0, there is a minimum, so the minima are equally spaced in sin θ, except either side of the central maximum.
We can note too that, for light diffracting the throught slits, the slit is usually much wider than a wavelength, so the pattern is usually very small, so the approximation that sin θ = θ is usually good. Next we calculate how the intensity varies with sin θ.