Velocity Distribution of Gas molecules :
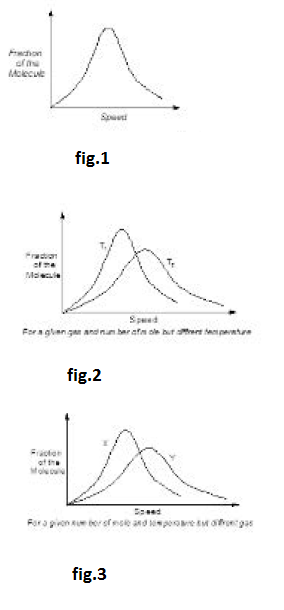
Speed of a gas molecule changes continuously due to the intermolecular collisions and their collisions with the wall of container. Thus, speed of an individual molecule is not constant. Also, the observable properties of gas such as volume, pressure and temperature are constant with time. It is expected to be applicable to the distribution of molecular speed and we consider a statistical average of the speed of whole of the collection of gas molecules to remain constant with time. That is the fraction or the total molecules having speed between any definite ranges must be constant, even though the speeds of the individual molecules may be changing as a result of molecular collisions. Distribution of molecular speed over a possible range was first investigated by Maxwell using the theory of probability. Results were expressed as the Maxwell law for distribution of molecular speed as shown in fig.1.
`dN_u = 4 pi N (M/(2 pi RT))^(3/2) e^((-m u^2)/(2RT)) u^2 du`
`= 4 pi N (M/(2 pi kT))^(3/2) e^((-m u^2)/(2kT)) u^2 du`
The above expression gives the number of molecules `dN_u` having speeds between `u` and `u + du` in term of total number of molecules present (`N`), molar mass (`M`) of gas and temperature (`T`). According to expression the fraction of molecules `((dN_u) /N)` having the speeds in the range of `u` and `u + du`, for a gas of molar mass (`M`) depends only on temperature. Hence, for a given temperature, this fraction is constant. A plot of fraction of molecules in the speed range `u` and `u + du`, `1/N ((dNu)/(du))` vs `u` is described in the graph. The peaks in the curve correspond to a speed, which is possessed by maximum fraction of molecules, called "most probable speed".
`ast` `text(Some conclusive points for distribution of molecular Speeds are)` :
(i) The fraction of molecules having either very high or very low speeds is very small. Majority of molecules have speed near to `U_(rnps)` in the middle of the range of molecular speeds. See fig.2.
(ii) The total area under the curve in fig.3 is a measure of total number of molecules in collection.
(iii) Since, rise in temperature raises the kinetic energy of gas molecules, it follows that fractions of molecules having lower speed range decreases and fraction of molecules having higher speed range increases. Also the curve at higher temperature has its `U_(mps)` shifted to higher value but the corresponding fractions of molecules have decreased. Thus in general, the distribution of speeds is wider at higher temperature than at lower temperature as shown in figure `(T_2 >T_1)`.
(iv) Distribution of molecular speed also depends upon the mass of gas molecule. At similar temperature, a heavier gas molecule has a narrow distribution of speeds than a lighter gas molecule as shown in the following diagram `(M_x > M_y)` :
As per kinetic theory of gases, each molecule is moving with altogether different velocity. Let `n` molecules be present in a given mass of gas, in which `n_1` molecules have a speed of `v_1`, `n_2` molecules have a speed of `v_2`, `n_n` molecules have a speed of `v_n`.
The average velocity or `U_(av) =` average of all such velocity terms.
Average velocity `= (n_1u_1 + n_2u_2 + n_3u_3 + ............+n_n u_n)/n`
Using Maxwell distribution average velocity is determined as `U_(av) = srqt((8RT)/(pi M))`
Another mean velocity proposed by Maxwell was `U_(rms)` as the square root of means of square of all such velocities.
`U_(rms) = sqrt((n_1 u_1^2 + n_2 u_2^2 +.....................+ n_n u_n^2)/n)`
Using Maxwell distribution `rms` velocity is determined as `U_(rms) = sqrt((3RT)/M)`
Most probable speed is the velocity which is possessed by maximum no. of molecules. `U_(mp) = sqrt((2RT)/M)`
Furthermore `U_(mp) : U_(av) : U_(rms) : : sqrt((2RT)/M) : sqrt((8RT)/(piM)) : sqrt((3RT)/M) = sqrt2 : sqrt(8/pi) : sqrt3 = 1 : 1.128 : 1.224`
Also `U_(av) = U_(rms) xx0.9213`
`ast` `text(For calculating) V_(rms), V_(mp), text(or) V_(av)` by above relations the value of `M` should be used in `kg`/`mol` and `R` should be taken as `8.314` `J`/`K` `mol` to get velocity in `m`/`s`.
`dN_u = 4 pi N (M/(2 pi RT))^(3/2) e^((-m u^2)/(2RT)) u^2 du`
`= 4 pi N (M/(2 pi kT))^(3/2) e^((-m u^2)/(2kT)) u^2 du`
The above expression gives the number of molecules `dN_u` having speeds between `u` and `u + du` in term of total number of molecules present (`N`), molar mass (`M`) of gas and temperature (`T`). According to expression the fraction of molecules `((dN_u) /N)` having the speeds in the range of `u` and `u + du`, for a gas of molar mass (`M`) depends only on temperature. Hence, for a given temperature, this fraction is constant. A plot of fraction of molecules in the speed range `u` and `u + du`, `1/N ((dNu)/(du))` vs `u` is described in the graph. The peaks in the curve correspond to a speed, which is possessed by maximum fraction of molecules, called "most probable speed".
`ast` `text(Some conclusive points for distribution of molecular Speeds are)` :
(i) The fraction of molecules having either very high or very low speeds is very small. Majority of molecules have speed near to `U_(rnps)` in the middle of the range of molecular speeds. See fig.2.
(ii) The total area under the curve in fig.3 is a measure of total number of molecules in collection.
(iii) Since, rise in temperature raises the kinetic energy of gas molecules, it follows that fractions of molecules having lower speed range decreases and fraction of molecules having higher speed range increases. Also the curve at higher temperature has its `U_(mps)` shifted to higher value but the corresponding fractions of molecules have decreased. Thus in general, the distribution of speeds is wider at higher temperature than at lower temperature as shown in figure `(T_2 >T_1)`.
(iv) Distribution of molecular speed also depends upon the mass of gas molecule. At similar temperature, a heavier gas molecule has a narrow distribution of speeds than a lighter gas molecule as shown in the following diagram `(M_x > M_y)` :
As per kinetic theory of gases, each molecule is moving with altogether different velocity. Let `n` molecules be present in a given mass of gas, in which `n_1` molecules have a speed of `v_1`, `n_2` molecules have a speed of `v_2`, `n_n` molecules have a speed of `v_n`.
The average velocity or `U_(av) =` average of all such velocity terms.
Average velocity `= (n_1u_1 + n_2u_2 + n_3u_3 + ............+n_n u_n)/n`
Using Maxwell distribution average velocity is determined as `U_(av) = srqt((8RT)/(pi M))`
Another mean velocity proposed by Maxwell was `U_(rms)` as the square root of means of square of all such velocities.
`U_(rms) = sqrt((n_1 u_1^2 + n_2 u_2^2 +.....................+ n_n u_n^2)/n)`
Using Maxwell distribution `rms` velocity is determined as `U_(rms) = sqrt((3RT)/M)`
Most probable speed is the velocity which is possessed by maximum no. of molecules. `U_(mp) = sqrt((2RT)/M)`
Furthermore `U_(mp) : U_(av) : U_(rms) : : sqrt((2RT)/M) : sqrt((8RT)/(piM)) : sqrt((3RT)/M) = sqrt2 : sqrt(8/pi) : sqrt3 = 1 : 1.128 : 1.224`
Also `U_(av) = U_(rms) xx0.9213`
`ast` `text(For calculating) V_(rms), V_(mp), text(or) V_(av)` by above relations the value of `M` should be used in `kg`/`mol` and `R` should be taken as `8.314` `J`/`K` `mol` to get velocity in `m`/`s`.