Liquefaction of Gases :
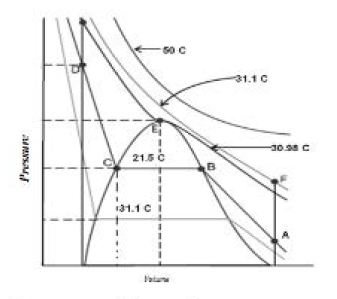
First complete data on pressure-volume-temperature relations or a substance in both gaseous and liquid state was obtained by `text(Thomas Andrews)` on carbon dioxide. He plotted isotherms of carbon dioxide at various temperatures. Later on it was found that real gases behave in the same manner as carbon dioxide. Andrews noticed that at high temperatures isotherms look like that of an ideal gas and the gas cannot be liquefied even at very high pressure. As the temperature is lowered, shape of the curve changes and data shows considerable deviation from ideal behaviour. At `30.98^oC` carbon dioxide remains gas upto `73` atm pressures. At `73` atm pressure, liquid carbon dioxide appears for the first time. The temperature `30.98^oC` is called `text(critical temperature) (T_c)` of carbon dioxide.
The critical temperature, pressure and volume are called critical constants. Further increase in pressure simlply compresses the liquid carbon dioxide and the curve represents the compressibility of the liquid. The steep line represents the isotherm of liquid. Even a slight compression results in steep rise in pressure indicating very low compressibility of the liquid. Below `30.98^oC`, the behavior of the gas on compression is quite different. At `21.5^oC`, carbon dioxide remains as a gas only upto point `B`. At point `B`, liquid of a particular volume appears. Further compression does not change the pressure. Liquid and gaseous carbon dioxide coexist and further application of pressure results in the condensation of more gas until the point `C` is reached. At point `C`, all the gas has been condensed and further application of pressure merely compresses the liquid as shown by steep line. Below `30.98^oC` each curve shows the similar trend. Only length of the horizontal line increases at lower temperatures. At critical point horizontal portion of the isotherm merges into one point.
So at point `E = ((delP)/(del V))_(T_c) =0` and `((del^2P)/delV^2)_(T_c) =0`
Critical temperature `T_c` is the maximum temperature at which a gas can be liquefied, i.e. the temperature above which a liquid cannot exist.
Critical pressure `P_c` is the minimum pressure required to cause liquefaction at the temperature `T_c`.
Critical volume `V_c` is the volume occupied by one mole of a gas at critical temperature `T_c` and critical pressure `P_c�`. The point `E` in Fig. represents the gas in its critical state. At this point the temperature, pressure and volume have critical values. These three are known as critical constants. The isotherm corresponding to the temperature `T_c` is known as critical isotherm. To the left of the point `E` on this isotherm, we have the liquid state whereas to the right, we have the gaseous state. Thus, at point `E` transition from liquid to gaseous state (or vice versa) takes place and thus it is not possible to state whether the substance is in the gaseous form or in the liquid form. In fact, both the states become indistinguishable at the critical point. The surface of separation between liquid and gas disappears. At this point the various physical properties such as density, refractive index, etc., have identical values for both the states.
`((del p)/(delV))_T = 0` and the condition that this slope has a maximum value of `del/(delV){((delp)/(delV))_T}_T =0`
From the van der Waals equation
`p = (RT)/(V_m -b) - a/(V_m^2)`, we get
`((delp)/delV_m)_T = (2RT)/(V_m-b)^2 + (2a)/(V_m^3 `
`((del^2p)/(delV_m^2))_T = (2RT)/(V_m -b)^3 - (6a)/(V_m^4)`
Hence at the critical point, ` - (RT_c)/(V_c -b)^2 + (2a)/(V_c^3) =0`
and `- (2 RT)/(V_c -b)^3 + (6a)/V_c^4 =0`
Solving Eqs for `V_c` and `T_c`, we get `V_c = 3b`
`T_c = (8a)/(27 Rb)`
Substituting the values of `V_c` and `T_c` in the van der Waals equation, we have
`p_c = (RT_c)/(V_c -b) =a/V_c^2 = (R((8a)/(27Rb)))/(3b -b) - a/(3b)^2`
`= (4a)/(27b^2) - a/(9b^2) = a/(27b^2)`
The critical temperature, pressure and volume are called critical constants. Further increase in pressure simlply compresses the liquid carbon dioxide and the curve represents the compressibility of the liquid. The steep line represents the isotherm of liquid. Even a slight compression results in steep rise in pressure indicating very low compressibility of the liquid. Below `30.98^oC`, the behavior of the gas on compression is quite different. At `21.5^oC`, carbon dioxide remains as a gas only upto point `B`. At point `B`, liquid of a particular volume appears. Further compression does not change the pressure. Liquid and gaseous carbon dioxide coexist and further application of pressure results in the condensation of more gas until the point `C` is reached. At point `C`, all the gas has been condensed and further application of pressure merely compresses the liquid as shown by steep line. Below `30.98^oC` each curve shows the similar trend. Only length of the horizontal line increases at lower temperatures. At critical point horizontal portion of the isotherm merges into one point.
So at point `E = ((delP)/(del V))_(T_c) =0` and `((del^2P)/delV^2)_(T_c) =0`
Critical temperature `T_c` is the maximum temperature at which a gas can be liquefied, i.e. the temperature above which a liquid cannot exist.
Critical pressure `P_c` is the minimum pressure required to cause liquefaction at the temperature `T_c`.
Critical volume `V_c` is the volume occupied by one mole of a gas at critical temperature `T_c` and critical pressure `P_c�`. The point `E` in Fig. represents the gas in its critical state. At this point the temperature, pressure and volume have critical values. These three are known as critical constants. The isotherm corresponding to the temperature `T_c` is known as critical isotherm. To the left of the point `E` on this isotherm, we have the liquid state whereas to the right, we have the gaseous state. Thus, at point `E` transition from liquid to gaseous state (or vice versa) takes place and thus it is not possible to state whether the substance is in the gaseous form or in the liquid form. In fact, both the states become indistinguishable at the critical point. The surface of separation between liquid and gas disappears. At this point the various physical properties such as density, refractive index, etc., have identical values for both the states.
`((del p)/(delV))_T = 0` and the condition that this slope has a maximum value of `del/(delV){((delp)/(delV))_T}_T =0`
From the van der Waals equation
`p = (RT)/(V_m -b) - a/(V_m^2)`, we get
`((delp)/delV_m)_T = (2RT)/(V_m-b)^2 + (2a)/(V_m^3 `
`((del^2p)/(delV_m^2))_T = (2RT)/(V_m -b)^3 - (6a)/(V_m^4)`
Hence at the critical point, ` - (RT_c)/(V_c -b)^2 + (2a)/(V_c^3) =0`
and `- (2 RT)/(V_c -b)^3 + (6a)/V_c^4 =0`
Solving Eqs for `V_c` and `T_c`, we get `V_c = 3b`
`T_c = (8a)/(27 Rb)`
Substituting the values of `V_c` and `T_c` in the van der Waals equation, we have
`p_c = (RT_c)/(V_c -b) =a/V_c^2 = (R((8a)/(27Rb)))/(3b -b) - a/(3b)^2`
`= (4a)/(27b^2) - a/(9b^2) = a/(27b^2)`