We will now extend the definition of trigonometric ratios to any angle in terms of radian measure and study them as trigonometric functions.

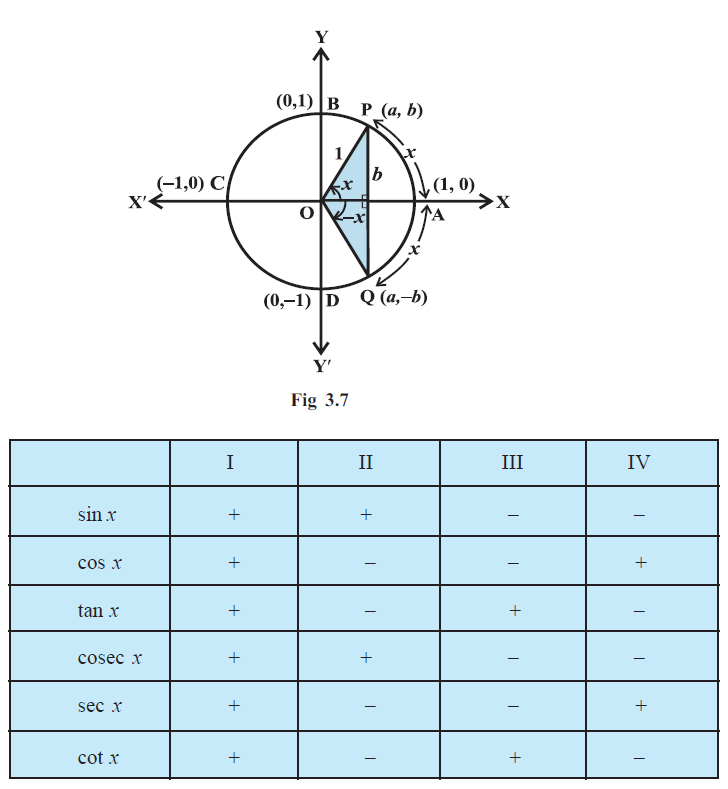
Consider a unit circle with centre at origin of the coordinate axes.

Let `P (a, b)` be any point on the circle with angle `AOP = x` radian, i.e., length of arc `AP = x` (Fig 3.6).

We define cos x = a and sin x = b Since ΔOMP is a right triangle, we have

` \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ color(blue)(OM^2 + MP^2 = OP^2) ` or `color(green)(a^2 + b^2 = 1)`

Thus, for every point on the unit circle, we have

` \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \color(green)(a^2 + b^2 = 1)` or `color(red)(cos^2 x + sin^2 x = 1)`

`=>` Since one complete revolution subtends an angle of `2π` radian at the centre of the circle, `color(purple)(∠AOB =π/2),` `color(purple)(∠AOC = π)` and `color(purple)(∠AOD = 3π /2) .`

`color(blue)(=>"All angles which are integral multiples of"\ \ π /2 "are called quadrantal angles.")`

The coordinates of the points `A, B, C` and `D` are, respectively, `(1, 0), (0, 1), (–1, 0)` and `(0, –1).` Therefore, for quadrantal angles, we have

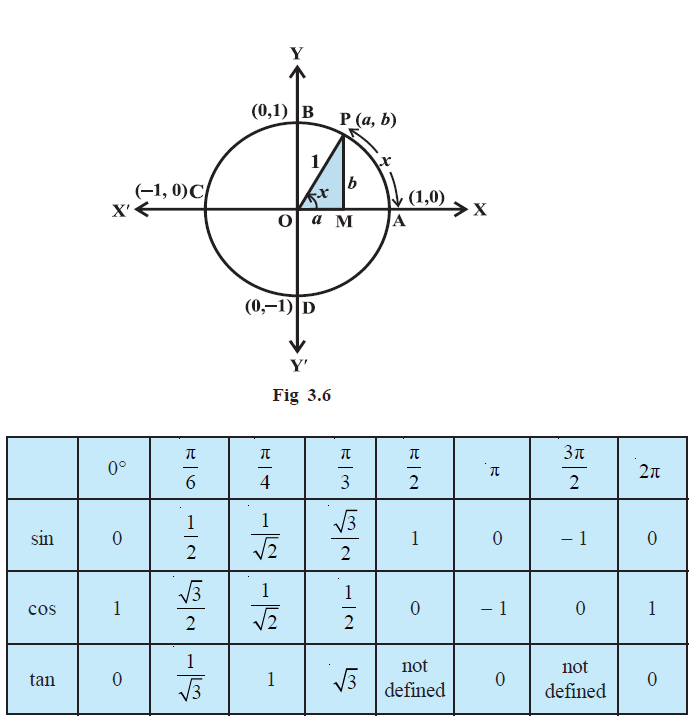
` \ \ \ \ \ \ \ \ \ color(green)(cos 0° = 1 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ sin 0° = 0,)`

` \ \ \ \ \ \ \ \ \color(green)( cos (π/ 2) = 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ sin (π /2) = 1)`

` \ \ \ \ \ \ \ \ \color(green)(cosπ = − 1 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \sinπ = 0)`

` \ \ \ \ \ \ \ \ \color(green)(cos ((3π)/2 )= 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ sin((3π)/2) = –1)`

` \ \ \ \ \ \ \ \ \color(green)( cos 2π = 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ sin 2π = 0)`


Now, if we take one complete revolution from the point P, we again come back to same point `P.` Thus, we also observe that if `x` increases (or decreases) by `color(blue)("any integral multiple of 2π")` `color(red)("the values of sine and cosine functions do not change.")` Thus,

` \ \ \ \ \ \ \ \ \ \ \ \ \ color(red)(sin (2nπ + x) = sin x, n ∈ Z , \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ cos (2nπ + x) = cos x , n ∈ Z)`

Further, `color(green)(sin x = 0),` if `color(green)(x = 0, ± π, ± 2π , ± 3π, ........,)` i.e., when `x` is an integral multiple of `π`

and `color(green)(cos x = 0)` , if `color(green)(x = pm pi/2 , pm (3 pi)/2 , pm (5 pi)/2)`,.... i.e., `cos x` vanishes when `x` is an odd multiple of `π/2` . Thus

` color(red)(sin x = 0)` implies `color(red)(x = nπ)`, where `n` is any integer

` color(red)(cos x = 0)` implies ` color(red)(x = (2n + 1)π/2)` , where `n` is any integer.

We now define other trigonometric functions in terms of sine and cosine functions:

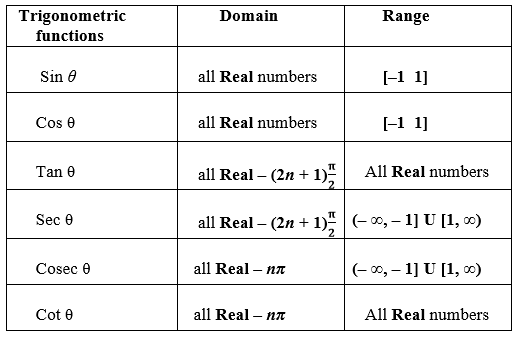
` color(red)(cosec x = 1/(sin x)) , \ \ color(blue)(x ≠ nπ)` , where `n` is any integer.

` color(red)(sec x = 1/(cos x)) , \ \ color(blue)(x ≠ (2n +1 ) pi/2)` , where `n` is any integer

` color(red)(tan x = (sin x)/(cos x) ), \ \ color(blue)(x ≠ (2n +1) pi/2 )`, where `n` is any integer.

` color(red)(cot x = ( cos x)/(sin x)), \ \ color(blue)(x ≠ n π)`, where `n` is any integer

We have shown that for all real `x`

`color(purple)( sin^2 x + cos^2 x = 1)`

`color(purple)(1 + tan^2 x = sec^2 x)`

`color(purple)(1 + cot^2 x = cosec^2 x)`

Let `P (a, b)` be a point on the unit circle with centre at the origin such that `∠AOP = x.` If `∠AOQ = – x,` then the coordinates of the point `Q` will be `(a, –b)` (Fig 3.7). Therefore

`color(blue)(cos (– x) = cos x)`

and `color(blue)(sin (– x) = – sin x)`

Since for every point `P (a, b)` on the unit circle, `– 1 ≤ a ≤ 1` and `– 1 ≤ b ≤ 1,`

we have `– 1 ≤ cos x ≤ 1` and `–1 ≤ sin x ≤ 1` for all `x.`

`=>` In the `color(green)(ul"first quadrant"\ \ ( 0 < x < pi/2)) , ` `color(red)(a)` and `color(red)(b)` are both positive,

`=>` In the `color(green)(ul"second quadrant" \ \ ( pi/2 < x < pi )) , ` `color(red)(a)` is negative and `color(red)(b)` is positive,

`=>` In the `color(green)(ul"third quadrant" \ \ (pi < x < (3pi)/2 )), ` `color(red)(a)` and `color(red)(b)` are both negative and

`=>` In the `color(green)(ul"fourth quadrant" \ \ ( (3 pi)/2 < x < 2 pi )), ` `color(red)(a)` is positive and `color(red)(b)` is negative.

Therefore, `sin x` is positive for `0 < x < π,` and negative for `π < x < 2π.`

Similarly, `cos x` is positive for `0 < x < pi/2` , negative for ` pi/2< x < (3 pi)/2` and also positive for `(3 pi)/2 < x < 2 pi` .

Likewise, we can find the signs of other trigonometric

functions in different quadrants. In fact, we have the following table.

From the definition of sine and cosine functions, we observe that they are defined for all real numbers.

`=>` Further, We observe that for each real number `x,`

`color(purple)(– 1 ≤ sin x ≤ 1)` and `color(purple)(– 1 ≤ cos x ≤ 1)`

`=>` Thus, `color(purple)(ul"domain")` of `color(red)(y = sin x)` and `color(red)(y = cos x)` is the `color(blue)("set of all real numbers")` and `color(purple)(ul"range")` is the interval `color(blue){([–1, 1])},` i.e., `– 1 ≤ y ≤ 1.`

`=>` Since `color(red)(cosec x =1/(sin x ))` , the domain of `y = cosec x` is the set `{ x : x ∈ R` and `x ≠ n π, n ∈ Z}` and range is the set `{y : y ∈ R, y ≥ 1` or `y ≤ – 1}.`

Similarly, the domain of

`=>` `color(red)(y = sec x)` is the set `{x : x ∈ R` and `x ≠ (2n + 1) π/2 , n ∈ Z}` and `color(purple)("range")` is the set `{y : y ∈ R, y ≤ – 1` or `y ≥ 1}.`

`=>` The domain of `color(red)(y = tan x)` is the set `{x : x ∈ R` and `x ≠ (2n + 1) π/2 , n ∈ Z}` and `color(purple)("range")` is the `color(blue)("set of all real numbers")`.

`=>` The domain of `color(red)(y = cot x)` is the set `{x : x ∈ R` and `x ≠ n π, n ∈ Z}` and the `color(purple)("range")` is the `color(blue)("set of all real numbers")`.