`\color{blue} ✍️` In this Section, we shall derive expressions for trigonometric functions of the sum and difference of two numbers (angles) and related expressions.

The basic results in this connection are called trigonometric identities. We have seen that
`1. \ \ color{red}(sin (– x) = – sin x)`
`2. \ \ color{red}( cos (– x) = cos x)`

We shall now prove some more results:

`3. \ \ color{red}( cos (x + y) = cos x cos y – sin x sin y)`

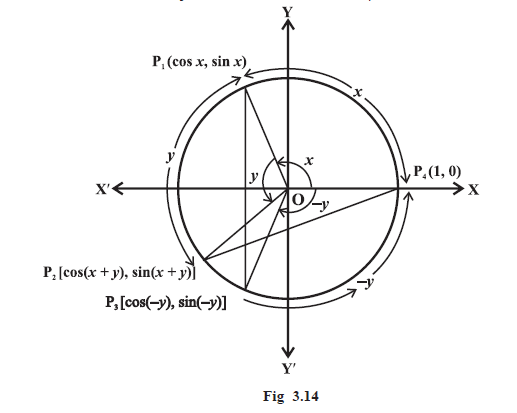
`\color{blue} ✍️` Consider the unit circle with centre at the origin. Let `x` be the angle `color{red}(P_4OP_1)` and `y` be the angle `color{red}(P_1OP_2)`. Then `color{red}((x + y))` is the angle `color{red}(P_4OP_2)`. Also let `color{red}((– y))` be the angle `color{red}(P_4OP_3)`.

`\color{blue} ✍️` Therefore, `P_1, P_2, P_3` and `P_4` will have the coordinates `color{red}(P_1 \ \(cos x, sin x), ``color{greeen}[ P_2 \ \ [cos (x + y), sin (x + y)]]`,`color{purple}[ P_3 \ \ [cos (– y), sin (– y)]]` and `color{red}(P_4 \ \ (1, 0))` (Fig 3.14).


Consider the triangles `color{red}(P_1OP_3)` and `color{red}(P_2OP_4)`. They are congruent Therefore,

`color{red}(1P_1P_3)` and `color{red}(1P_2P_4)` are equal. By using distance formula, we get

`color{red}(1P_1P_3^2 = [cos x – cos (– y)]^2 + [sin x – sin(–y)^2]`

`\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \= (cos x – cos y)^2 + (sin x + sin y)^2`

`\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \= cos^2 + cos^2 y – 2 cos x cos y + sin^2 x + sin^2 y + 2sin x sin y`

`\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \= 2 – 2 (cos x cos y – sin x sin y)`

Also, `color{red}(P_2P_4^2 = [1 – cos (x + y)]^2 + [0 – sin (x + y)]^2)`

`\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \= 1 – 2cos (x + y) + cos^2 (x + y) + sin^2 (x + y)`

`\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \= 2 – 2 cos (x + y)`


Since `color{red}(P_1P_3 = P_2P_4,)` we have `color{red}(P_1P_3^2 = P_2P_4^2)`.

Therefore, `2 –2 (cos x cos y – sin x sin y) = 2 – 2 cos (x + y)`.

Hence `color{red}(cos (x + y) = cos x cos y – sin x sin y)`

Replacing `y` by `– y` in identity `cos (x + y) = cos x cos y – sin x sin y`, we get

`cos (x + (– y)) = cos x cos (– y) – sin x sin (– y)`

or `color{red}(cos (x – y) = cos x cos y + sin x sin y)`

If we replace `x` by `color{red}(pi/2)` and `y` by `x` in Identity (4), we get

`color{red}(cos (pi/2-x) = cos (pi/2) cos x + sin ( pi/2) sin x = sin x)`

Using the Identity 5, we have

`color{red}(sin (pi/2 -x) = cos [ pi/2 - (pi/2- x) ] = cos x)`

`color{blue}(sin (x+ y) = cos (pi/2 - (x+y) ) = cos ( (pi/2 -x ) - y ))`

`color{}(= cos (pi/2-x) cos y +sin (pi/2-x) sin y)`

`color{red}(= sin x cos y + cos x sin y)`

If we replace `y` by `–y,` in the Identity 7, we get the result .

`color(red)(sin (x – y) = sin x cos y – cos x sin y)`

`color{red}(cos ( pi/2 +x) = - sin x)`

`color{red}(sin (pi/2 +x) = cos x)`

`color{red}(cos (pi-x) = - cos x)`

`color{red}(sin (pi-x) = sin x)`

`color{red}(cos (π + x) = – cos x)`

`color{red}(sin (π + x) = – sin x)`

`color{red}(cos (2π – x) = cos x)`

`color{red}(sin (2π – x) = – sin x)`

Similar results for tan `x`, `cot x`, `sec x` and `cosec x` can be obtianed from the results of `sin x` and `cos x.`

Since none of the `color{red}(x, y)` and `color{red}((x + y))` is an odd multiple of `color{red}(π/2)` , it follows that `cos x,` `cos y` and `cos (x + y)` are non-zero. Now

`color{green}( tan (x + y) = (sin (x+y ) )/( cos (x+y) ) = (sin x cos y + cos x sin y )/( cos x cos y - sin x sin y ))`

Dividing numerator and denominator by `cos x` `cos y`, we have

`color{red}(tan (x+y) ) = ( (sin x cos y )/( cos x cos y ) + ( cos x sin y)/(cos x cos y) )/( (cos x cos y)/( cos x cos y ) - ( sin x sin y )/( cos x cos y) )`

` \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \color{red}(= (tan x + tan y )/(1- tan x tan y ))`

If we replace `y` by `– y` in Identity 10, we get

`color{blue}(tan (x – y) = tan [x + (– y)])`

` \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ color{red}(= (tan x+ tan (-y) )/( 1- tan x tan (-y) ) = (tan x - tan y)/(1+ tan x tan y ))`

`color{red}(cot (x+ y ) = (cot x cot y -1 )/( cot y + cot x))`

Since, none of the `x, y` and `(x + y)` is multiple of `π`, we find that `sin x` `sin y` and `sin(x + y)` are non-zero. Now,

`color{green}(cot (x+ y) = (cos (x+ y) )/(sin (x+ y) ) = (cos x cos y – sin x sin y)/( sin x cos y + cos x sin y))`

Dividing numerator and denominator by `sin x sin y,` we have

`color{red}( cot (x+ y) = (cot x cot y -1)/( cot y + cot x))`

If we replace `y` by `–y` in identity `12,` we get the result

`color(red)(cot (x – y)= (cot x cot y + 1)/(cot y - cot x))`

`\color{blue} ✍️` We know that

`color{green}(cos (x + y) = cos x cos y – sin x sin y)`

`\color{blue} ✍️` Replacing `y` by `x,` we get

`color{red}(cos 2x )= cos^2x – sin^2 x = 2 cos^2 x – 1`

` \ \ \ \ \ \ \ \ = cos^2 x – (1 – cos^2 x) =color{red}( 2 cos^2x – 1)`

`\color{blue} ✍️` Again, `color{green}(cos 2x = cos^2 x – sin^2 x)`

` \ \ \ \ \ \ \ \ \ \ = 1 – sin^2 x – sin^2 x = color{red}( 1 – 2 sin^2 x)`.

`\color{blue} ✍️` We have `color{green}(cos 2x = cos^2 x – sin^2 x = (cos^2 x - sin^2 x)/( cos^2 x + sin^2 x))`

Dividing each term by `color{orange}(cos^2 x,)` we get

`color{red}(cos 2x = (1- tan^2 x)/(1+ tan^2 x))`

`\color{blue} ✍️` We have

`color{red}(sin (x + y) = sin x cos y + cos x sin y)`

`\color{blue} ✍️` Replacing `y` by `x,`

we get `color{red}(sin 2x = 2 sin x cos x.)`

`\color{blue} ✍️` Again `color{green}(sin 2x = (2 sin x cos x)/( cos^2 x + sin^2 x))`

Dividing each term by `color{red}(cos^2 x)`, we get

`color{red}(sin 2x = (2 tan x )/( 1+ tan^2 x))`

`\color{blue} ✍️` We know that

`color{green}(tan (x+y) = (tan x + tan y )/( 1- tan x tan y))`

Replacing `y` by `x` ,

we get `color{red}(tan 2x = (2 tan x)/(1 - tan^2 x))`

`\color{blue} ✍️` We have,

`color{green}(sin 3x = sin (2x + x))`

` \ \ \ \ \ \ \ \ \ \ \= sin 2x cos x + cos 2x sin x`

`\ \ \ \ \ \ \ \ \ \ \= 2 sin x cos x cos x + (1 – 2sin^2 x) sin x`

`\ \ \ \ \ \ \ \ \ \ \= 2 sin x (1 – sin^2 x) + sin x – 2 sin^3 x`

`\ \ \ \ \ \ \ \ \ \ \= 2 sin x – 2 sin^3 x + sin x – 2 sin^3 x`

`\ \ \ \ \ \ \ \ \ \ \ color{red}(= 3 sin x – 4 sin^3 x)`

`\color{blue} ✍️` We have,

`color{green}(cos 3x = cos (2x +x))`

`\ \ \ \ \ \ \ \ \ \ \= cos 2x cos x – sin 2x sin x`

`\ \ \ \ \ \ \ \ \ \ \= (2cos^2 x – 1) cos x – 2sin x cos x sin x`

`\ \ \ \ \ \ \ \ \ \ \= (2cos^2 x – 1) cos x – 2cos x (1 – cos^2 x)`

`\ \ \ \ \ \ \ \ \ \ \= 2cos^3 x – cos x – 2cos x + 2 cos^3 x`

`\ \ \ \ \ \ \ \ \ \ \ color{red}(= 4 cos^3 x – 3cos x)`.

`\color{blue} ✍️` We have

`color{red}(tan3x =tan (2x + x))`

`\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ color{green}(= (tan 2x +tanx)/( 1- tan 2x tan x))`

` \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = ( (2 tan x)/( 1- tan^2 x) + tan x)/( 1- ( 2 tan x * tan x )/(1- tan^2 x) )`

` \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \=(2 tan x + tan x - tan^3 x)/(1- tan^2 x -2 tan^2 x) `

`\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ color{red}( = (3 tan x - tan^3 x)/( 1- 3 tan^2 x))`

(i) `color{red}(cos x + cos y = 2 cos( (x+y)/2) cos ((x-y)/2))`

(ii) `color{red}(cos x – cos y = -2 sin ((x+y)/2) sin ((x-y)/2))`

(iii) `color{red}(sin x + sin y = 2 sin ((x+y)/2 ) cos ((x-y)/2))`

(iv) `color{red}(sin x – sin y = 2 cos ((x+y)/2) sin ((x-y)/2))`

`\color{blue} ✍️` We know that

`color{green}(cos (x + y) = cos x cos y – sin x sin y) .................................................... (1)`

and `color{green}(cos (x – y) = cos x cos y + sin x sin y ).............................................. (2)`

`color{blue}("Adding and subtracting (1) and (2)")`, we get

`color{orange}(cos (x + y) + cos(x – y) = 2 cos x cos y) .................................... (3)`

and `color{orange}(cos(x + y) – cos (x – y) = – 2 sin x sin y) .....................................................(4)`

`\color{blue} ✍️` We know that

`color{green}(sin (x + y) = sin x cos y + cos x sin y) .................................................. (5)`

and sin `color{green}((x – y) = sin x cos y – cos x sin y) .............................................. (6)`

`color{blue}("Adding and subtracting (5) and (6)")`, we get

`color{orange}(sin (x + y) + sin (x – y) = 2 sin x cos y) ................................................ (7)`

`color{orange}(sin (x + y) – sin (x – y) = 2cos x sin y) .............................................. (8)`

Let `color{red}(x + y = θ and x – y = φ.)` Therefore

`color{red}(x= ( ( θ +φ )/2 ))` and `color{red}(y = ( (θ -φ )/ 2))`

Substituting the values of `x` and `y` in `(3), (4), (7)` and `(8),` we get

`color{red}(cos θ + cos φ = 2 cos ( ( θ +φ)/2 ) cos ((θ -φ)/2 ))`

`color{red}(cos θ – cos φ = – 2 sin ( ( θ +φ )/2) sin ( ( θ -φ)/2))`

`color{red}(sin θ + sin φ = 2 sin ( ( θ +φ )/2 ) cos ( ( θ - φ)/2))`

`color{red}(sin θ – sin φ = 2 cos ( (θ +φ )/2) sin ( ( θ - φ)/2 ))`

Since `θ` and `φ` can take any real values, we can replace `θ` by `x` and `φ` by `y.`
Thus, we get

`color{red}(cos x + cos y = 2 cos( (x+y)/2) cos ((x-y)/2)) ; \ \ \ \ \ \ \ \ \ \color{red}(cos x – cos y = -2 sin ((x+y)/2) sin ((x-y)/2))` ,

`color{red}(sin x + sin y = 2 sin ((x+y)/2 ) cos ((x-y)/2)) ; \ \ \ \ \ \ \ \ \ \ \ color{red}(sin x – sin y = 2 cos ((x+y)/2) sin ((x-y)/2))` .

(i) `color{red}(2 cos x cos y = cos (x + y) + cos (x – y))`

(ii) `color{red}(–2 sin x sin y = cos (x + y) – cos (x – y))`

(iii) `color{red}(2 sin x cos y = sin (x + y) + sin (x – y))`

(iv) `color{red}(2 cos x sin y = sin (x + y) – sin (x – y))`.